Question

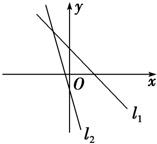已知直线l₁，l₂的方程分别为x+ay+b=0，x+cy+d=0，其图象如图所示，则有（　　）

• A、ac＜0
• B、a＜c
• C、bd＜0
• D、b＞d

Answer 1

分析：把两条直线的方程化为斜截式方程，根据图象得到斜率的大小以及与y轴截距的大小即可列出两个不等式，化简不等式即可得到字母的符号及大小．

解答：解：直线方程化为l₁：y=-

1

a

x-

b

a

，l₂：y=-

1

c

x-

d

c

．
由图象知，-

1

c

＜-

1

a

＜0，-

b

a

＞0＞-

d

c

，
∴a＞c＞0，b＜0，d＞0．
故选C

点评：考查学生会根据图象判断同一坐标系中两直线的斜率和截距的大小，做题时注意数形结合．