题目内容

9．在等差数列{an}中，a1=3，a1+a3=14，则公差d=4，an=4n-1．

分析 设数列{an}的公差为d，利用等差数列的通项公式代入a1+a3=14，列出有关d和a1的方程，由此解得d的值，可得an．

解答 解：设数列{an}的公差为d，由a1+a3=14，可得2a1+2d=14，
即a1+d=7，把a1=3代入，解得d=4，
所以an=3+4（n-1）=4n-1．
故答案为：4；4n-1．

点评 本题主要考查等差数列的通项公式的应用，属于基础题．

练习册系列答案
相关题目
20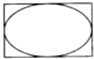．如图所示，矩形长为6，宽为4，在矩形内随机的撒2400颗黄豆，数得落在椭圆外的黄豆数为516颗，依据此实验数据可以估计出椭圆的面积约为（　　）
A．17.84B．18.84C．5.16D．6.16
20．偶函数y=f（x）的图象关于直线x=2对称，f（3）=3，则f（-1）=3．
17．已知集合A={0，a}，B={-1，1}，若A∩B={-1}，则A∪B=（　　）
A．{0，1}B．{-1，0}C．{-1，1}D．{-1，0，1}
4．已知直线y=kx+3与圆x2+y2-6x-4y+5=0相交于M，N两点，若|MN|=2$\sqrt{3}$，则k的值是-2或$\frac{1}{2}$．
14．已知i是虚数单位，则|$\frac{1-i}{1+i}$|=（　　）
A．0B．1C．2D．3
1．已知i为虚数单位，则复数$\frac{1-3i}{1+i}$=（　　）
A．2+iB．2-iC．-1-2iD．-1+2i
18．两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为（　　）
A．akmB．$\sqrt{2}$akmC．2akmD．$\sqrt{3}$akm
16．设f（n）=1+$\frac{1}{2}$+$\frac{1}{8}$+…+$\frac{1}{2n-1}$（n∈N*），那么f（n+1）-f（n）=$\frac{1}{2n+1}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网