题目内容
已知平面上三个向量|
|=|
|=|
|=2,它们之间的夹角都是120°.
(I)求
•
的值.
(II)求证:(
-
)⊥
.
| a |
| b |
| c |
(I)求
| a |
| c |
(II)求证:(
| a |
| b |
| c |
分析:(I)直接代入向量的数量积的定义
•
=|
||
|cos120°可求
(II)要证明(
-
)⊥
,只要证明(
-
)•
=0即可
| a |
| c |
| a |
| c |
(II)要证明(
| a |
| b |
| c |
| a |
| b |
| c |
解答:解:(I)
•
=|
||
|cos120°=2×2×(-
)=-2
(II)∵(
-
)•
=
•
-
•
=|
||
|cos120°-|
||
|cos120°
=2×2×(-
)-2×2×(-
)=0
∴(
-
)⊥
.
| a |
| c |
| a |
| c |
| 1 |
| 2 |
(II)∵(
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
| c |
| b |
| c |
=2×2×(-
| 1 |
| 2 |
| 1 |
| 2 |
∴(
| a |
| b |
| c |
点评:本题主要考查了向量的数量积的定义及性质的简单应用,属于基础试题

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
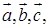 的模均为1,它们相互之间的夹角均为
的模均为1,它们相互之间的夹角均为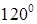 。
。 ;
;
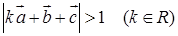 ,求
,求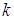 的取值范围。
的取值范围。