题目内容
已知| |=3,|
|=3,|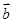 |=4,向量
|=4,向量 +
+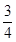
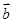 与
与 -
-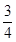
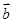 的位置关系为( )
的位置关系为( )
A.平行 B.垂直 C.夹角为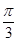 D.不平行也不垂直
D.不平行也不垂直
【答案】
B
【解析】
试题分析:因为|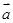 |=3,|
|=3,|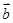 |=4,所以(
|=4,所以(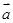 +
+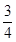
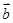 )·(
)·(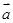 -
-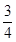
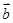 )=
)=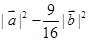 =0,即向量
=0,即向量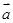 +
+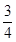
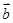 与
与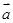 -
-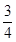
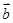 的位置关系为垂直,选B。
的位置关系为垂直,选B。
考点:本题主要考查平面向量的数量积,向量垂直的条件。
点评:简单题,两向量垂直,则它们的数量积为0.

练习册系列答案
相关题目
已知
<α<π,tanα+cotα=-
,则tanα的值为( )
| 3π |
| 4 |
| 10 |
| 3 |
| A、-3 | ||
B、-
| ||
C、-3或-
| ||
D、-
|