题目内容
不等式(x-1)•|x|≥0的解集是
- A.{x|x>1}
- B.{x|x≥1}
- C.{x|x>1或x=0}
- D.{x|x≥1或x=0}
D
分析:根据绝对值的代数意义分两种情况考虑:1、x大于0时,利用正数的绝对值等于它的本身,把原不等式化为一元二次不等式,根据两数相乘同号得正得出x与x-1同号,化为两个一元一次不等式组即可求出x的范围;当x小于等于0,根据负数的绝对值等于它的相反数及0的绝对值还是0,化简原不等式,再利用两数相乘异号得负得出x与x-1异号,化为两个一元一次不等式,即可求出x的范围,综上,得到原不等式的解集.
解答:分两种情况考虑:
当x>0时,|x|=x,
原不等式化简得:x(x-1)≥0,
可化为: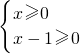 或
或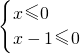 ,
,
解得:x≥1或x≤0(舍去),
原不等式的解集为x≥1;
当x≤0时,|x|=-x,
原不等式化简得:-x(x-1)≥0,即x(x-1)≤0,
可化为: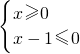 或
或 ,
,
解得:0≤x≤1,又x≤0,
原不等式解集为x=0,
综上,原不等式的解集为{x|x≥1或x=0}.
故选D
点评:此题考查了其他不等式的解法,涉及的知识有绝对值的代数意义,两数相乘同号得正异号得负的取符号法则,以及一元一次不等式的解法,利用了转化及分类讨论的思想,是高考常考的题型.
分析:根据绝对值的代数意义分两种情况考虑:1、x大于0时,利用正数的绝对值等于它的本身,把原不等式化为一元二次不等式,根据两数相乘同号得正得出x与x-1同号,化为两个一元一次不等式组即可求出x的范围;当x小于等于0,根据负数的绝对值等于它的相反数及0的绝对值还是0,化简原不等式,再利用两数相乘异号得负得出x与x-1异号,化为两个一元一次不等式,即可求出x的范围,综上,得到原不等式的解集.
解答:分两种情况考虑:
当x>0时,|x|=x,
原不等式化简得:x(x-1)≥0,
可化为:
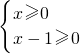 或
或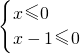 ,
,解得:x≥1或x≤0(舍去),
原不等式的解集为x≥1;
当x≤0时,|x|=-x,
原不等式化简得:-x(x-1)≥0,即x(x-1)≤0,
可化为:
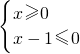 或
或 ,
,解得:0≤x≤1,又x≤0,
原不等式解集为x=0,
综上,原不等式的解集为{x|x≥1或x=0}.
故选D
点评:此题考查了其他不等式的解法,涉及的知识有绝对值的代数意义,两数相乘同号得正异号得负的取符号法则,以及一元一次不等式的解法,利用了转化及分类讨论的思想,是高考常考的题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目