题目内容
已知函数y=Asin(ωx+ϕ),x∈R(其中A>0,ω>0,0<φ<π)在一个周期内的图象如图,(1)求函数的解析式;
(2)当
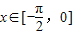 时,求函数的最值.
时,求函数的最值.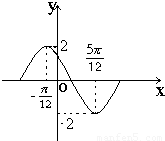
【答案】分析:(1)由图可知A=2,由 T=
T=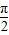 可求ω,由-
可求ω,由-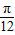 ω+φ=2kπ+
ω+φ=2kπ+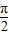 (k∈Z)及0<φ<π可求得φ;
(k∈Z)及0<φ<π可求得φ;
(2)由x∈[-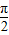 ,0]⇒2x+
,0]⇒2x+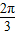 ∈[-
∈[-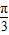 ,
,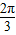 ]⇒sin(2x+
]⇒sin(2x+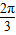 )∈[-
)∈[-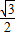 ,1],从而可求函数的最值.
,1],从而可求函数的最值.
解答:解:(1)由图知A=2,
∵ T=
T=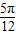 -(-
-(-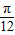 )=
)=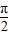 ,故T=
,故T=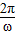 =π,
=π,
∴ω=2,
∵函数y=2sin(2x+ϕ)经过点(-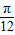 ,2),
,2),
∴-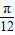 ×2+φ=2kπ+
×2+φ=2kπ+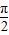 (k∈Z),
(k∈Z),
∴φ=2kπ+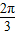 (k∈Z),
(k∈Z),
又0<φ<π,
∴φ=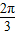 .
.
∴y=2sin(2x+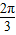 );
);
(2)∵x∈[-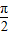 ,0]
,0]
∴2x+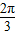 ∈[-
∈[-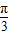 ,
,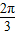 ],
],
∴-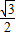 ≤sin(2x+
≤sin(2x+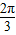 )≤1,
)≤1,
∴-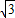 ≤f(x)=2sin(2x+
≤f(x)=2sin(2x+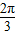 )≤2,
)≤2,
∴当x∈[-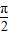 ,0]时,f(x)max=2,f(x)min=-
,0]时,f(x)max=2,f(x)min=-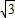 .
.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的单调性与值域,属于中档题.
 T=
T=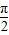 可求ω,由-
可求ω,由-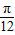 ω+φ=2kπ+
ω+φ=2kπ+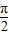 (k∈Z)及0<φ<π可求得φ;
(k∈Z)及0<φ<π可求得φ;(2)由x∈[-
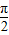 ,0]⇒2x+
,0]⇒2x+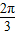 ∈[-
∈[-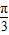 ,
,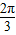 ]⇒sin(2x+
]⇒sin(2x+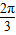 )∈[-
)∈[-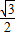 ,1],从而可求函数的最值.
,1],从而可求函数的最值.解答:解:(1)由图知A=2,
∵
 T=
T=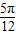 -(-
-(-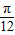 )=
)=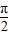 ,故T=
,故T=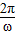 =π,
=π,∴ω=2,
∵函数y=2sin(2x+ϕ)经过点(-
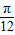 ,2),
,2),∴-
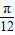 ×2+φ=2kπ+
×2+φ=2kπ+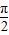 (k∈Z),
(k∈Z),∴φ=2kπ+
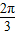 (k∈Z),
(k∈Z),又0<φ<π,
∴φ=
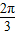 .
.∴y=2sin(2x+
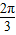 );
);(2)∵x∈[-
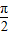 ,0]
,0]∴2x+
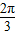 ∈[-
∈[-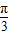 ,
,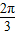 ],
],∴-
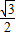 ≤sin(2x+
≤sin(2x+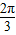 )≤1,
)≤1,∴-
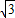 ≤f(x)=2sin(2x+
≤f(x)=2sin(2x+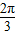 )≤2,
)≤2,∴当x∈[-
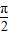 ,0]时,f(x)max=2,f(x)min=-
,0]时,f(x)max=2,f(x)min=-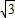 .
.点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的单调性与值域,属于中档题.

练习册系列答案
相关题目
已知函数y=Asin(ωx+φ),在同一周期内,当x=
时,取最大值y=2,当x=
时,取得最小值y=-2,那么函数的解析式为( )
| π |
| 12 |
| 7π |
| 12 |
A、y=
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
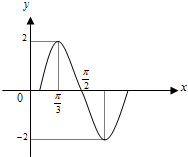 已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )
已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )A、y=2sin(
| ||||
B、y=2sin(3x+
| ||||
C、y=2sin(3x-
| ||||
D、y=2sin(3x-
|
 已知函数
已知函数 已知函数
已知函数