题目内容
已知数列{an}满足条件:a1=1,a2=r(r>0)且{an·an+1}是公比为q(q>0)的等比数列,设bn=a2n-1+a2n(n=1,2,…)
(Ⅰ)求出使不等式anan+1+an+1an+2>an+2an+2(n∈N*)成立的q的取值范围;
(Ⅱ)求bn和![]() ,其中Sn=b1+b2+…+bn;
,其中Sn=b1+b2+…+bn;
(Ⅲ)设r=219.2-1,q=![]() ,求数列{
,求数列{![]() }的最大项和最小项的值.
}的最大项和最小项的值.
答案:
解析:
解析:
解:(Ⅰ)由题意得rqn-1+rqn>rqn+1 由题设r>0,q>0,故上式q2-q-1<0 所以 由于q>0,故0<q< (Ⅱ)因为 所以 b1=1+r≠0,所以{bn}是首项为1+r,公比为q的等比数列, 从而bn=(1+r)qn-1 当q=1时,Sn=n(1+r)
当0<q<1时,Sn=
当q>1时,Sn= 综上所述 (Ⅲ)由(Ⅱ)知bn=(1+r)qn-1
从上式可知当n-20.2>0时n≥21(n∈N)时,cn随n的增大而减小,故 1<cn<c21=1+ 当n-20.2<0,即n≤20(n∈N)时,cn也随着n的增大而减小,故 1>cn>c20=1+ 综合①、②两式知对任意的自然数n有c20≤cn≤c21 故{cn}的最大项c21=2.25,最小项c20=-4.
|

练习册系列答案
相关题目
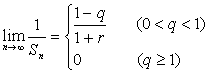

 ,且an=
,且an=
 =
= ,则数列{an}是 ( )
,则数列{an}是 ( )