Question

已知数列｛a_n｝满足：a₁＝，且a_n＝

（1）   求数列｛a_n｝的通项公式；

（2）   证明：对于一切正整数n，不等式a₁·a₂·……a_n<2·n！

 

Answer 1

【答案】

（1）a_n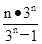＝（n³1）   （2）略

【解析】本试题主要是考查了数列的通项公式的求解和数列求和的综合运用。

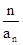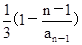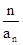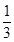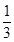（1）因为将条件变为：1－＝，因此｛1－｝为一个等比数列，其首项为1－＝，公比，从而1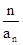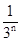－＝，据此得a_n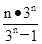＝（n³1）

（2）据1°得，a₁·a₂·…a_n＝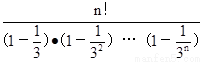

为证a₁·a₂·……a_n<2·n！

只要证nÎN^*时有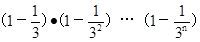>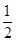只要用数学归纳法证明即可。