题目内容
已知函数f(x)=ax2+kbx(x>0)与函数g(x)=ax+blnx,a、b、k为常数,它们的导函数分别为y=f′(x)与y=g′(x)(1)若g(x)图象上一点p(2,g(2))处的切线方程为:x-2y+2ln2-2=0,求a、b的值;
(2)对于任意的实数k,且a、b均不为0,证明:当ab>0时,y=f′(x)与y=g′(x)的图象有公共点;
(3)在(1)的条件下,设A(x1,y1),B(x2,y2),(x1<x2)是函数y=g(x)的图象上两点,
 ,证明:x1<x<x2.
,证明:x1<x<x2.
【答案】分析:(1)由g(x)=ax+blnx,知g(2)=2a+bln2,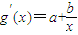 ,
, ,故g(x)图象上一点p(2,g(2))处的切线方程为y-2a-bln2=(a+
,故g(x)图象上一点p(2,g(2))处的切线方程为y-2a-bln2=(a+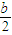 )(x-2),由此能求出a和b.
)(x-2),由此能求出a和b.
(2)由f(x)=ax2+kbx(x>0),利用导数的性质和韦达定理能够证明当ab>0时,y=f′(x)与y=g′(x)的图象有公共点.
(3)由a=0,b=1,知g(x)=lnx,由此进行分类讨论,能够证明x1<x<x2.
解答:解:(1)∵g(x)=ax+blnx,
∴g(2)=2a+bln2,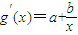 ,
,
∴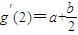 ,
,
∴g(x)图象上一点p(2,g(2))处的切线方程为:
y-2a-bln2=(a+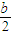 )(x-2),
)(x-2),
整理,得(a+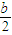 )x-y+bln2-b=0,
)x-y+bln2-b=0,
∵g(x)图象上一点p(2,g(2))处的切线方程为:x-2y+2ln2-2=0,
∴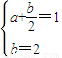 ,解得a=0,b=1.
,解得a=0,b=1.
(2)∵f(x)=ax2+kbx(x>0),
f′(x)=2ax+kb,
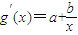 ,
,
原题即为ab>0时,?k∈R有方程2ax+kb-a-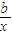 =0,
=0,
即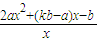 =0在x>0时有解.
=0在x>0时有解.
∴2ax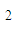 +(kb-a)x-b=0在x>0时有解,
+(kb-a)x-b=0在x>0时有解,
∵两根之积为:-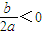 ,
,
△=(kb-a)2+8ab
=k2b2-2abk+a2+8ab,k∈R,
∴△′=4a2b2-4b2(a2+8ab)
=4a2b2-4a2b2-32ab3
=-32ab3<0,
∴方程2ax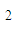 +(kb-a)x-b=0在x>0时有解,
+(kb-a)x-b=0在x>0时有解,
∴ab>0时,y=f′(x)与y=g′(x)的图象有公共点.
(3)∵a=0,b=1,
∴g(x)=lnx,x>0
∴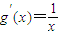 ,
,
∴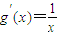 =
=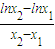 ,
,
∴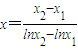 =
=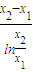 ,
,
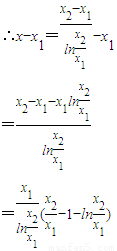
令t=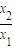 ,则t>1,令h(t)=t-1-lnt,
,则t>1,令h(t)=t-1-lnt,
则h′(x)=1- =
=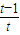 >0,
>0,
∴h(t)在(1,+∞)上单调递增,
∴x-x1>0,即x>x1.
同理可得:x2>x,
综上述:x1<x<x2.
点评:本题考查实数值的求法,考查图象的公共点的证明,考查不等式的证明.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
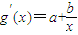 ,
, ,故g(x)图象上一点p(2,g(2))处的切线方程为y-2a-bln2=(a+
,故g(x)图象上一点p(2,g(2))处的切线方程为y-2a-bln2=(a+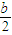 )(x-2),由此能求出a和b.
)(x-2),由此能求出a和b.(2)由f(x)=ax2+kbx(x>0),利用导数的性质和韦达定理能够证明当ab>0时,y=f′(x)与y=g′(x)的图象有公共点.
(3)由a=0,b=1,知g(x)=lnx,由此进行分类讨论,能够证明x1<x<x2.
解答:解:(1)∵g(x)=ax+blnx,
∴g(2)=2a+bln2,
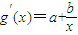 ,
,∴
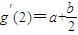 ,
,∴g(x)图象上一点p(2,g(2))处的切线方程为:
y-2a-bln2=(a+
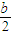 )(x-2),
)(x-2),整理,得(a+
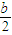 )x-y+bln2-b=0,
)x-y+bln2-b=0,∵g(x)图象上一点p(2,g(2))处的切线方程为:x-2y+2ln2-2=0,
∴
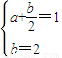 ,解得a=0,b=1.
,解得a=0,b=1.(2)∵f(x)=ax2+kbx(x>0),
f′(x)=2ax+kb,
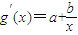 ,
,原题即为ab>0时,?k∈R有方程2ax+kb-a-
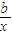 =0,
=0,即
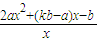 =0在x>0时有解.
=0在x>0时有解.∴2ax
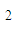 +(kb-a)x-b=0在x>0时有解,
+(kb-a)x-b=0在x>0时有解,∵两根之积为:-
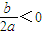 ,
,△=(kb-a)2+8ab
=k2b2-2abk+a2+8ab,k∈R,
∴△′=4a2b2-4b2(a2+8ab)
=4a2b2-4a2b2-32ab3
=-32ab3<0,
∴方程2ax
 +(kb-a)x-b=0在x>0时有解,
+(kb-a)x-b=0在x>0时有解,∴ab>0时,y=f′(x)与y=g′(x)的图象有公共点.
(3)∵a=0,b=1,
∴g(x)=lnx,x>0
∴
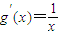 ,
,∴
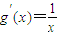 =
=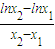 ,
,∴
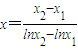 =
=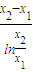 ,
,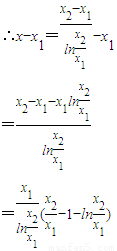
令t=
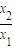 ,则t>1,令h(t)=t-1-lnt,
,则t>1,令h(t)=t-1-lnt,则h′(x)=1-
 =
=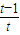 >0,
>0,∴h(t)在(1,+∞)上单调递增,
∴x-x1>0,即x>x1.
同理可得:x2>x,
综上述:x1<x<x2.
点评:本题考查实数值的求法,考查图象的公共点的证明,考查不等式的证明.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目