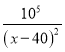题目内容
【题目】已知![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,记
时,记![]() ,已知
,已知![]() 有三个极值点,求
有三个极值点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,
时,![]() 在
在![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;(Ⅱ)
单调递减;(Ⅱ)![]() ,且
,且![]() .
.
【解析】
试题分析:(Ⅰ)由![]() ,分
,分![]() 、
、![]() 讨论;(Ⅱ)由已知
讨论;(Ⅱ)由已知![]() ,
,
则![]() ,若
,若![]() 有三个极值点,则
有三个极值点,则![]() 有两个不为
有两个不为![]() 且不为1的相异实根,令
且不为1的相异实根,令![]() ,由函数值分布值,若
,由函数值分布值,若![]() 有两个相异实根,则
有两个相异实根,则![]() ,∴
,∴![]() ,又
,又![]() 及
及![]() 时,
时,![]() ,故
,故![]() 的取值范围为
的取值范围为![]() ,且
,且![]() .
.
试题解析:(Ⅰ)∵![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
所以,当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 单调递增.
单调递增.
当![]() 时,令
时,令![]() ,∴
,∴![]() ,
,
![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 单调递增.
单调递增.
![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 单调递减.
单调递减.
(Ⅱ)当![]() 时,
时,![]() .
.
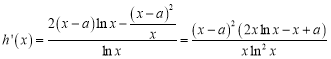 .
.
∵![]() 有三个极值点,∴
有三个极值点,∴![]() 有三个相异的实根.
有三个相异的实根.
所以![]() 有两个不为
有两个不为![]() 且不为1的相异实根.
且不为1的相异实根.
令![]() ,令
,令![]() ,∴
,∴![]() ,列表得
,列表得
|
|
|
|
|
| - | 0 | + | + |
| 单调递减 | 单调递增 | 单调递增 |
![]() 时,
时,![]() ,
,![]() 时,
时,![]()
大致图象为

若![]() 有两个相异实根,则
有两个相异实根,则![]() ,∴
,∴![]() ,
,
若![]() ,则
,则![]() ,因为
,因为![]() 的根不为
的根不为![]() ,所以
,所以![]() .
.
若![]() ,则
,则![]() ,因为
,因为![]() 的根不为1,所以
的根不为1,所以![]() .
.
综上![]() ,且
,且![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目