题目内容
P1（2，-1），P2（0，5），且P在P1P2的延长线上，使|
|=2|
|，则点P为（ ）A．（2，11）
B．（
，3）C．（
，3）D．（2，-7）
【答案】分析：根据P在P1P2的延长线上，由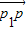
、
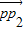共线可得答案．
解答：解：由题意知P1P2=P2P，
设P（x，y），则（-2，6）=（x，y-5），
∴
，∴
，
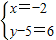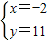∴点P的坐标为（-2，11）．
故选A．
点评：本题主要考查向量的共线问题．
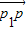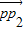、共线可得答案．解答：解：由题意知P1P2=P2P，
设P（x，y），则（-2，6）=（x，y-5），
∴
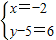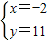，∴，∴点P的坐标为（-2，11）．
故选A．
点评：本题主要考查向量的共线问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
P1（2，-1），P2（0，5），且P在P1P2的延长线上，使|
|=2|
|，则点P为（ ）
| p1p |
| p p2 |
| A、（2，11） | ||
B、（
| ||
C、（
| ||
| D、（2，-7） |
所成的比为λ，则下列结论中：
的内分点；②若λ＜-1，则点P在
的延长线上；③若-1＜λ＜0,则点P在
的反向延长线上；④若λ=0，则点P与点P1重合；⑤若λ=-1,则点P与点P2重合．
（n∈N*）．当n→+∞时，点Pn无限趋近于点M，则点M的坐标为 ．