题目内容
【题目】已知函数f(x)=loga(ax2﹣x+1),其中a>0且a≠1.
(1)当a= ![]() 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)当f(x)在区间 ![]() 上为增函数时,求实数a的取值范围.
上为增函数时,求实数a的取值范围.
【答案】
(1)解:当 ![]() 时,
时, ![]() 恒成立,
恒成立,
故定义域为R,
又∵ ![]() ,且函数
,且函数 ![]() 在(0,+∞)单调递减,
在(0,+∞)单调递减,
∴ ![]() ,即函数f(x)的值域为(﹣∞,1]
,即函数f(x)的值域为(﹣∞,1]
(2)解:依题意可知,
i)当a>1时,由复合函数的单调性可知,必须ax2﹣x+1在 ![]() 上递增,且ax2﹣x+1>0对
上递增,且ax2﹣x+1>0对 ![]() 恒成立.
恒成立.
故有 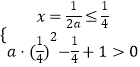 ,解得:a≥2;
,解得:a≥2;
ii)当0<a<1时,同理必须ax2﹣x+1在 ![]() 上递减,且ax2﹣x+1>0对
上递减,且ax2﹣x+1>0对 ![]() 恒成立.
恒成立.
故有 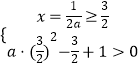 ,解得:
,解得: ![]() .
.
综上,实数a的取值范围为 ![]()
【解析】(1)当a=![]() 时,可判断出函数f(x)的定义域为R,结合复合函数的单调性,不难得出f(x)的值域,(2)对a进行分类讨论,结合复合函数的单调性,解出a的取值范围.
时,可判断出函数f(x)的定义域为R,结合复合函数的单调性,不难得出f(x)的值域,(2)对a进行分类讨论,结合复合函数的单调性,解出a的取值范围.
【考点精析】利用函数的值域和复合函数单调性的判断方法对题目进行判断即可得到答案,需要熟知求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”.

练习册系列答案
相关题目