题目内容
已知直线l:y=kx+b,曲线M:y=|x2-2|.
(1)若k=1,直线与曲线恰有三个公共点,求实数b的值;
(2)若b=1,直线与曲线M的交点依次为A,B,C,D四点,求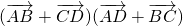 的取值范围.
的取值范围.
解:(1)分两种情况:
①直线y=x+b与抛物线y=-x2+2在(- ,
, )内相切,即方程x2+x+b-2=0在(-
)内相切,即方程x2+x+b-2=0在(- ,
, )内有△=0,
)内有△=0,
由△=1-4b+8=0,得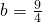 ,符合.
,符合.
②直线y=x+b过点(- ,0),即0=-
,0),即0=- +b,得
+b,得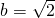 .
.
综上知,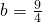 或
或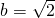
(2)根据直线y=kx+1与曲线M有四个交点可得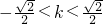
由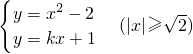 ,得x2-kx-3=0,
,得x2-kx-3=0,
则有: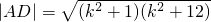 ,其中
,其中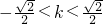 .
.
由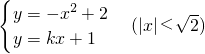 ,得x2+kx-1=0,
,得x2+kx-1=0,
则有: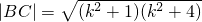 ,其中
,其中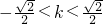 .
.
所以
=(k2+1)(k2+12)-(k2+1)(k2+4)=8(k2+1),
∵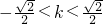 ,∴8(k2+1)∈[8,12),
,∴8(k2+1)∈[8,12),
∴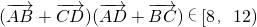
分析:(1)分两种情况:①直线y=x+b与抛物线y=-x2+2在(- ,
, )内相切;②直线y=x+b过点(-
)内相切;②直线y=x+b过点(- ,0),即可确定实数b的值;
,0),即可确定实数b的值;
(2)根据直线y=kx+1与曲线M有四个交点确定k的范围,由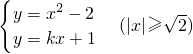 ,计算|AD|;由
,计算|AD|;由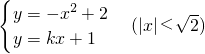 ,计算|BC|,利用
,计算|BC|,利用 ,即可求得结论.
,即可求得结论.
点评:本题考查带绝对值的函数,考查直线与曲线的位置关系,考查向量知识的运用,正确转化是关键.
①直线y=x+b与抛物线y=-x2+2在(-
 ,
, )内相切,即方程x2+x+b-2=0在(-
)内相切,即方程x2+x+b-2=0在(- ,
, )内有△=0,
)内有△=0,由△=1-4b+8=0,得
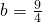 ,符合.
,符合.②直线y=x+b过点(-
 ,0),即0=-
,0),即0=- +b,得
+b,得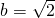 .
.综上知,
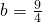 或
或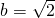
(2)根据直线y=kx+1与曲线M有四个交点可得
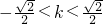
由
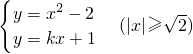 ,得x2-kx-3=0,
,得x2-kx-3=0,则有:
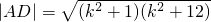 ,其中
,其中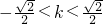 .
.由
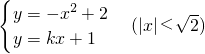 ,得x2+kx-1=0,
,得x2+kx-1=0,则有:
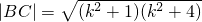 ,其中
,其中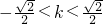 .
.所以

=(k2+1)(k2+12)-(k2+1)(k2+4)=8(k2+1),
∵
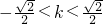 ,∴8(k2+1)∈[8,12),
,∴8(k2+1)∈[8,12),∴
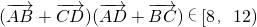
分析:(1)分两种情况:①直线y=x+b与抛物线y=-x2+2在(-
 ,
, )内相切;②直线y=x+b过点(-
)内相切;②直线y=x+b过点(- ,0),即可确定实数b的值;
,0),即可确定实数b的值;(2)根据直线y=kx+1与曲线M有四个交点确定k的范围,由
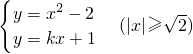 ,计算|AD|;由
,计算|AD|;由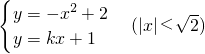 ,计算|BC|,利用
,计算|BC|,利用 ,即可求得结论.
,即可求得结论.点评:本题考查带绝对值的函数,考查直线与曲线的位置关系,考查向量知识的运用,正确转化是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足
如图所示,已知圆M:(x+1)2+y2=8及定点N(1,0),点P是圆M上一动点,点Q为PN的中点,PM上一点G满足