题目内容
5.已知函数f(x)=2cos2$\frac{x}{2}-\sqrt{3}$sinx.(Ⅰ)求函数f(x)的最小正周期和单调递增区间;
(Ⅱ)若α为第二象限角,且$f(α-\frac{π}{3})=\frac{1}{3}$,求$\frac{cos2α}{1+cos2α-sin2α}$的值.
分析 (Ⅰ)化简函数f(x),利用正弦函数的图象与性质求出它的最小正周期与单调递增区间;
(Ⅱ)根据α为第二象限角,且$f(α-\frac{π}{3})=\frac{1}{3}$,求出sinα、cosα的值,计算$\frac{cos2α}{1+cos2α-sin2α}$的值即可.
解答 解:(Ⅰ)∵函数f(x)=2cos2$\frac{x}{2}-\sqrt{3}$sinx
=2×$\frac{1+cosx}{2}$-$\sqrt{3}$sinx
=cosx-$\sqrt{3}$sinx+$\frac{1}{2}$
=-2($\frac{\sqrt{3}}{2}$sinx-$\frac{1}{2}$cosx)+$\frac{1}{2}$
=-2sin(x-$\frac{π}{6}$)+$\frac{1}{2}$;
∴函数f(x)的最小正周期为T=2π,
令$\frac{π}{2}$+2kπ≤x-$\frac{π}{6}$≤$\frac{3π}{2}$+2kπ,k∈Z,
∴$\frac{2π}{3}$+2kπ≤x≤$\frac{5π}{3}$+2kπ,k∈Z,
∴f(x)的单调递增区间为[$\frac{2π}{3}$+2kπ,$\frac{5π}{3}$+2kπ],k∈Z;
(Ⅱ)∵α为第二象限角,且$f(α-\frac{π}{3})=\frac{1}{3}$,
∴-2sin(α-$\frac{π}{6}$-$\frac{π}{3}$)+$\frac{1}{2}$=-2sin(α-$\frac{π}{2}$)+$\frac{1}{2}$=2sin($\frac{π}{2}$-α)=2cosα+$\frac{1}{2}$=$\frac{1}{3}$,
∴cosα=-$\frac{1}{12}$,
∴sinα=$\frac{\sqrt{143}}{12}$,
∴$\frac{cos2α}{1+cos2α-sin2α}$=$\frac{{2cos}^{2}α-1}{{2cos}^{2}α-2sinαcosα}$
=$\frac{2{×(-\frac{1}{12})}^{2}-1}{2{×(-\frac{1}{12})}^{2}-2×\frac{\sqrt{143}}{12}×(-\frac{1}{12})}$
=$\frac{-71}{1+\sqrt{143}}$
=-$\frac{\sqrt{143}}{2}$+$\frac{1}{2}$.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了三角函数求值的应用问题,是综合性题目.

| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [75,90] | 5 | 0.05 |
| 第2组 | (90,105] | ① | 0.35 |
| 第3组 | (105,120] | 30 | ② |
| 第4组 | (120,135] | 20 | 0.20 |
| 第5组 | (135,150] | 10 | 0.10 |
| 合计 | 100 | 1.00 | |
(Ⅱ)为了能选拔出最优秀的学生参加数学竞赛,学校决定在成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮测试,求第3、4、5组每组各抽取多少名学生进入第二轮测试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生进行抽查,求第4组至少有一名学生被抽查的概率?
| A. | 243 | B. | 210 | C. | 150 | D. | 125 |
| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | -2 |
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
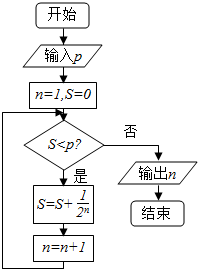
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
 某驾校为了保证学员科目二考试的通过率,要求学员在参加正式考试(下面简称正考)之前必须参加预备考试(下面简称预考),且在预考过程中评分标准得以细化,预考成绩合格者才能参加正考.现将10名学员的预考成绩绘制成茎叶图如图所示:
某驾校为了保证学员科目二考试的通过率,要求学员在参加正式考试(下面简称正考)之前必须参加预备考试(下面简称预考),且在预考过程中评分标准得以细化,预考成绩合格者才能参加正考.现将10名学员的预考成绩绘制成茎叶图如图所示: