题目内容
如图,已知平面a与平面交于a,b在b内.且b与a交于A,c在内,且c∥a,求证b、c是异面直线.

答案:
解析:
解析:
证法一:假设b、c不是异面直线,它们同在平面g内. ∵平面a、g均过直线c与点A, ∴a与g,a重合a在内.∴a在γ内. 又∵γ与b均过直线a与b, ∴b与γ重合,从而a与b重合,这与题设a与b交于a相矛盾. B、c是异面直线. 证法二:假设b、c不是异面直线,则b与c相交或平行. 若b与c相交,∵a∥c,a与b相交,从而a、b、c在同一平面内.即平面a与b重合,这与题设a与b交于a矛盾. 若b与c平行,∵a∥c,∴a∥b,这与题设a与b交于A矛盾. 综上可知,b与c是异面直线. 证法三:在b上取一点P(不同于A),则P ∵c 即b与c是异面直线. 点评:证明两条直线是异面直线通常用反证法,其中证法二列举了b、c不是异面直线的两种情况,相交或平行.证法三利用了教材第14页例3的结论,该结论就是异面直线的判定方法,以后再判定异面直线时,可直接利用这个结论.
|

练习册系列答案
相关题目
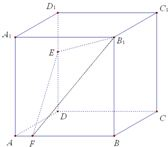 8、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A1C⊥平面B1EF;②△B1EF在侧面BCC1B1上 的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平 面B1EF与平面ABCD所成的二面角(锐角)的大小与点E的位置有关,与点F的位置无关,其中正确判断的个数有( )
8、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A1C⊥平面B1EF;②△B1EF在侧面BCC1B1上 的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平 面B1EF与平面ABCD所成的二面角(锐角)的大小与点E的位置有关,与点F的位置无关,其中正确判断的个数有( )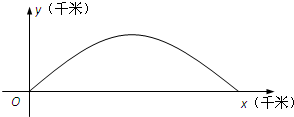 (2012•江苏)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
(2012•江苏)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-
