题目内容
已知直线l：y=x+m与椭圆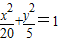
相交于不同的两点A，B，点M（4，1）为定点．（1）求m的取值范围；
（2）若直线l不过点M，求证：直线MA，MB与x轴围成一个等腰三角形．
【答案】分析：（1）直线方程代入椭圆方程，利用判别式大于0，即可求m的取值范围；
（2）证明直线MA、MB的倾斜角互补，即可证得结论．
解答：（1）解：直线l：y=x+m代入椭圆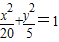
，可得5x2+8mx+4m2-20=0
∵直线l：y=x+m与椭圆
相交于不同的两点A，B，
∴△=64m2-20（4m2-20）＞0，
∴-5＜m＜5；
（2）证明：设直线MA、MB的斜率分别为k1，k2，点A（x1，y1），B（x2，y2），则x1+x2=-
，x1x2=
∴k1+k2=
+
=
=
=
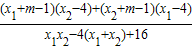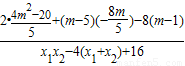=0
∴直线MA、MB的倾斜角互补，故直线MA，MB与x轴围成一个等腰三角形．
点评：本题考查直线与椭圆的位置关系，考查斜率的计算，属于基础题．
（2）证明直线MA、MB的倾斜角互补，即可证得结论．
解答：（1）解：直线l：y=x+m代入椭圆
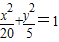，可得5x2+8mx+4m2-20=0∵直线l：y=x+m与椭圆
相交于不同的两点A，B，∴△=64m2-20（4m2-20）＞0，
∴-5＜m＜5；
（2）证明：设直线MA、MB的斜率分别为k1，k2，点A（x1，y1），B（x2，y2），则x1+x2=-
，x1x2=∴k1+k2=
+===
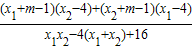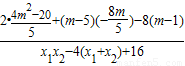=0∴直线MA、MB的倾斜角互补，故直线MA，MB与x轴围成一个等腰三角形．
点评：本题考查直线与椭圆的位置关系，考查斜率的计算，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
