题目内容
如图所示,定椭圆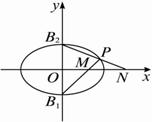
解析:取P(a,0),则M(a,0)、N(a,0),从而?|OM|·|ON|=a2;?
取P(c,![]() ),则M(
),则M(![]() ,0),N(
,0),N(![]() ,0).?
,0).?
故|OM|·|ON|=a2.?
于是猜想|OM|·|ON|=a2为定值.?
证明:设P(acosθ,bsinθ),其中|sinθ|≠1,?
且设M(x1,0),N(x2,0).?
∵三点B、M、P共线,且三点B2、N、P共线,?
∴![]() ,
,![]() ,?
,?
即x1=![]() ,x2=
,x2=![]() .?
.?
则|OM|·|ON|=|x1|·|x2|=|x1·x2|?
=|![]() |=|
|=|![]() |=a2(定值).?
|=a2(定值).?
故|OM|·|ON|为定值.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
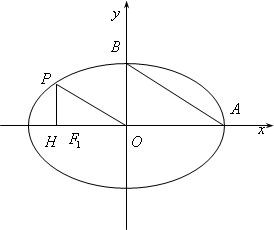 已知在椭圆
已知在椭圆 作斜率为
作斜率为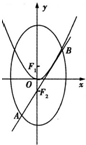 如图所示,椭圆C:
如图所示,椭圆C: