题目内容
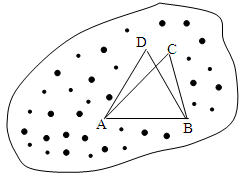
南充市某广场有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为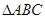 ,
, ,经测量
,经测量 米,
米, 米,
米,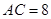 米,
米,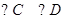 .
.
(Ⅰ)求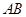 的长度;
的长度;
(Ⅱ)若环境标志的底座每平方米造价为5000元,不考虑其他因素,小李、小王谁的设计使建造费用最低(请说明理由)?最低造价为多少?( )
)
(Ⅰ)7米;(Ⅱ)小李的设计使建造费用最低,最低造价为86600元.
解析试题分析:(Ⅰ)分别在两个三角形中利用余弦定理即可解得;(Ⅱ)利用正弦定理求两个三角形的面积进行比较,面积小者造价则低,易求最低造价.
试题解析:(Ⅰ)在△ABC中,由余弦定理得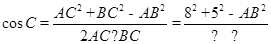 , 2分
, 2分
在 中,由余弦定理得
中,由余弦定理得 , 4分
, 4分
由 解得
解得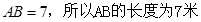 . 6分
. 6分
(Ⅱ)小李的设计使建造费用最低, 7分
理由为:已知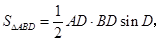

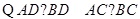 ,且
,且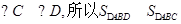 ,
,
故选择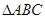 的形状建造环境标志费用较低, 9分
的形状建造环境标志费用较低, 9分
因为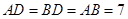 ,所以
,所以 是等边三角形,
是等边三角形,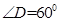 , 10分
, 10分
故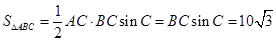 ,
,
所以所求最低造价为: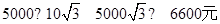 . 12分
. 12分
考点:1、余弦定理;2、正弦定理.

练习册系列答案
相关题目
 ABC中,内角A,B,C的对边分别为a,b,c.
ABC中,内角A,B,C的对边分别为a,b,c. ,
, .
. 的值; (Ⅱ)若
的值; (Ⅱ)若 ,求
,求 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 .
. 的值;
的值; ,求
,求 和
和 的值.
的值.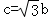 .
.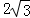 ,求a,b的值.
,求a,b的值.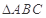 中,已知角
中,已知角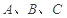 的对边分别为
的对边分别为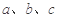 .向量
.向量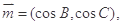
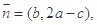 且向量
且向量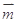 与
与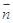 共线.
共线.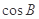 的值;
的值;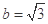 ,求
,求 中,
中, ,
, ,设
,设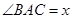 ,并记
,并记
 的解析式及其定义域;
的解析式及其定义域; ,若函数
,若函数 的值域为
的值域为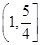 ,试求正实数
,试求正实数 的值
的值  中,已知
中,已知
 ;
; ,
, ,求
,求 .
. 中,
中, 边上的中线
边上的中线 长为3,且
长为3,且 ,
, .
.
 的值;(Ⅱ)求
的值;(Ⅱ)求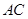 边的长.
边的长. 的角
的角 所对的边
所对的边 ,且
,且 .
. 的大小;
的大小; ,求
,求 的最大值并判断这时三角形的形状.
的最大值并判断这时三角形的形状.