题目内容
设f(x)的定义域为D,若f(x)满足下面两个条件,则称f(x)为闭函数.①f(x)在D内是单调函数;②存在[a,b]⊆D,使f(x)在[a,b]上的值域为[a,b].如果f(x)=
+k为闭函数,那么k的取值范围是( )
| 2x+1 |
A、-1<k≤-
| ||
B、
| ||
| C、k>-1 | ||
| D、k<1 |
分析:首先应根据条件将问题转化成:
=x-k在[-
,+∞)上有两个不等实根.然后,一方面:可以从数形结合的角度研究两函数y=
和y=x-k在[-
,+∞)上的交点个数问题,进而获得问题的解答;另一方面:可以化简方程
=x-k,得关于x的一元二次方程,从二次方程根的分布情况分析亦可获得问题的解答.
| 2x+1 |
| 1 |
| 2 |
| 2x+1 |
| 1 |
| 2 |
| 2x+1 |
解答:解:
方法一:因为:f(x)=
+k为[-
,+∞)上的增函数,又f(x)在[a,b]上的值域为[a,b],
∴
,即f(x)=x在[-
,+∞)上有两个不等实根,即
=x-k在[-
,+∞)上有两个不等实根.
∴问题可化为y=
和y=x-k在[-
,+∞)上有
两个不同交点.
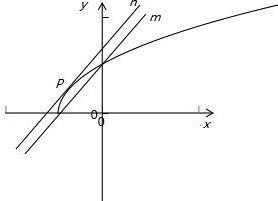
对于临界直线m,应有-k≥
,即k≤-
.
对于临界直线n,y′=(
)′=
,
令
=1,得切点P横坐标为0,
∴P(0,1),
∴n:y=x+1,令x=0,得y=1,∴-k<1,即k>-1.
综上,-1<k≤-
.
方法二:因为:f(x)=
+k为[-
,+∞)上的增函数,又f(x)在[a,b]上的值域为[a,b],
∴
,即f(x)=x在[-
,+∞)上有两个不等实根,即
=x-k在[-
,+∞)上有两个不等实根.
化简方程
=x-k,得x2-(2k+2)x+k2-1=0.
令g(x)=x2-(2k+2)x+k2-1,则由根的分布可得
,即
,
解得k>-1.又
=x-k,∴x≥k,∴k≤-
.
综上,-1<k≤-
,
故选A.
方法一:因为:f(x)=
| 2x+1 |
| 1 |
| 2 |
∴
|
| 1 |
| 2 |
| 2x+1 |
| 1 |
| 2 |
∴问题可化为y=
| 2x+1 |
| 1 |
| 2 |
两个不同交点.

对于临界直线m,应有-k≥
| 1 |
| 2 |
| 1 |
| 2 |
对于临界直线n,y′=(
| 2x+1 |
| 1 | ||
|
令
| 1 | ||
|
∴P(0,1),
∴n:y=x+1,令x=0,得y=1,∴-k<1,即k>-1.
综上,-1<k≤-
| 1 |
| 2 |
方法二:因为:f(x)=
| 2x+1 |
| 1 |
| 2 |
∴
|
| 1 |
| 2 |
| 2x+1 |
| 1 |
| 2 |
化简方程
| 2x+1 |
令g(x)=x2-(2k+2)x+k2-1,则由根的分布可得
|
|
解得k>-1.又
| 2x+1 |
| 1 |
| 2 |
综上,-1<k≤-
| 1 |
| 2 |
故选A.
点评:本题考查的是函数的最值及其几何意义.在解答的过程当中充分体现了问题转化的思想、数形结合的思想以及函数与方程的思想.同时二次函数根的分布情况对本体的解答也有相当大的作用.值得同学们体会和反思.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目