题目内容
如图
图
(1)求证:AE与⊙O相切于点A.
(2)当AB不是直径时,其他条件不变,结论还成立吗?若成立,请证明;若不成立,请说明理由.
(1)证明:∵AB是直径,
∴∠C=90°.
∴∠B+∠BAC=90°.
又∵∠B=∠CAE,∴∠BAC+∠CAE=90°.
∴AB⊥AE.
∴AE与⊙O相切于点A.
(2)解析:当AB不是直径时,结论仍然成立,如图

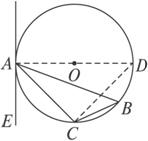
图
证明:连结AO,并延长AO交⊙O于点D,
∵AD是直径,∴∠D+∠DAC=90°.
又![]() =
=![]() ,∴∠B=∠D.
,∴∠B=∠D.
∵∠B=∠CAE,∴∠CAE+∠DAC=90°.
∴OA⊥AE.
∴AE与⊙O相切于点A.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 11、为了了解噪声污染的情况,某市环保局抽样调查了80个测量点的噪声声级(单位:分贝),并进行整理后分成五组,绘制出频率分布直方图,如图所示.已知从左至右前四组的频率分别是0.15,0.25,0.3,0.2,且噪声声级高于69.5分贝就会影响工作和生活,那么影响到工作和生活而需对附近区域进行治理的测量点有( )
11、为了了解噪声污染的情况,某市环保局抽样调查了80个测量点的噪声声级(单位:分贝),并进行整理后分成五组,绘制出频率分布直方图,如图所示.已知从左至右前四组的频率分别是0.15,0.25,0.3,0.2,且噪声声级高于69.5分贝就会影响工作和生活,那么影响到工作和生活而需对附近区域进行治理的测量点有( ) (2013•肇庆一模)(几何证明选讲选做题)
(2013•肇庆一模)(几何证明选讲选做题) (2011•滨州一模)我市某商场在春节促销活动中,对2011年2月2日10时至15时的销售额进行统计,其频率分布直方图如图所示,已知10时至11时销售额为3万元,则11时至13时的销售额为
(2011•滨州一模)我市某商场在春节促销活动中,对2011年2月2日10时至15时的销售额进行统计,其频率分布直方图如图所示,已知10时至11时销售额为3万元,则11时至13时的销售额为