题目内容
2.以F1(-1,0),F2(1,0)为焦点且与直线x-y+3=0有公共点的椭圆中,离心率最大的椭圆方程是( )| A. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{19}$=1 | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1 |
分析 设出椭圆的方程为$\frac{{x}^{2}}{{b}^{2}+1}+\frac{{y}^{2}}{{b}^{2}}=1$,求出离心率的平方,将直线方程代入椭圆方程得得到的关于x的一元二次方程的判别式大于0,求出 b2 的最小值,此时的离心率最大,离心率最大的椭圆方程可得.
解答 解:由题意知,c=1,a2-b2=1,故可设椭圆的方程为$\frac{{x}^{2}}{{b}^{2}+1}+\frac{{y}^{2}}{{b}^{2}}=1$,
离心率的平方为:$\frac{1}{{b}^{2}+1}$ ①,
∵直线x-y+3=0与椭圆有公共点,将直线方程代入椭圆方程得
(2b2+1)x2+6(b2+1)x+8b2+9-b4=0,
由△=36(b4+2b2+1)-4(2b2+1)( 8b2+9-b4 )≥0,
∴b4-3b2-4≥0,∴b2≥4,或 b2≤-1 (舍去),
∴b2 的最小值为4,
∴①的最大值为 $\frac{1}{5}$,此时,a2=b2+1=5,
∴离心率最大的椭圆方程是:$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1$,
故选:C.
点评 本题考查椭圆的标准方程和简单性质,利用直线和椭圆有交点可得判别式大于或等于0.求解b的最大值是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
12.下列函数中,既是偶函数又在(-∞,0)上单调递增的是( )
| A. | y=x2 | B. | y=2|x| | C. | y=sin x | D. | y=log2$\frac{1}{|x|}$ |
13.函数f(x)=(x-1)ln|x|的图象大致为( )
| A. |  | B. | 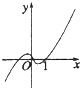 | C. | 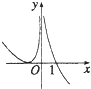 | D. | 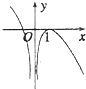 |