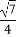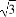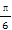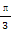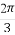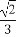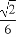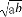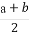题目内容
已知函数f(x)=sin sin(
sin(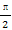 +
+ ).
).
(1)求函数f(x)在[-π,0]上的单调区间.
(2)已知角α满足α∈(0,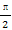 ),2f(2α)+4f(
),2f(2α)+4f(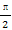 -2α)=1,求f(α)的值.
-2α)=1,求f(α)的值.
(1) 单调递减区间为[-π,- ],单调递增区间为[-
],单调递增区间为[- ,0]
,0]
(2) 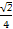
【解析】【思路点拨】(1)利用诱导公式及倍角公式化简f(x)的解析式后可求.
(2)利用已知将条件代入,整理成单角α的三角函数关系式后可解.
解:f(x)=sin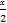 sin(
sin( +
+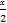 )
)
=sin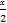 cos
cos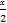 =
=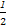 sinx.
sinx.
(1)函数f(x)的单调递减区间为[-π,- ],单调递增区间为[-
],单调递增区间为[- ,0].
,0].
(2)2f(2α)+4f( -2α)=1
-2α)=1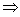 sin2α+2sin(
sin2α+2sin( -2α)=1
-2α)=1
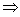 2sinαcosα+2(cos2α-sin2α)=1
2sinαcosα+2(cos2α-sin2α)=1
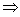 cos2α+2sinαcosα-3sin2α=0
cos2α+2sinαcosα-3sin2α=0
⇒(cosα+3sinα)(cosα-sinα)=0.
∵α∈(0, ),
),
∴cosα-sinα=0⇒tanα=1得α= ,故sinα=
,故sinα= ,
,
∴f(α)=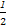 sinα=
sinα=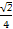 .
.

练习册系列答案
相关题目