题目内容
已知函数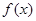 =
=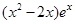 (e为自然对数的底数)
(e为自然对数的底数)
(Ⅰ)求函数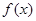 单调递增区间;(5分)
单调递增区间;(5分)
(Ⅱ)若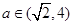 ,求函数
,求函数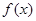 在区间[0,
在区间[0,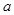 ]上的最大值和最小值.(5分)
]上的最大值和最小值.(5分)
(III) 若函数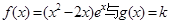 的图象有三个不同的交点,求实数k的取值范围.
的图象有三个不同的交点,求实数k的取值范围.
(参考数据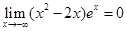 )(2分)
)(2分)
【答案】
解:(Ⅰ)对函数 求导,得
求导,得 =ex(x2-2).-----2分
=ex(x2-2).-----2分
∵ex>0. ∴g(x)=x2-2在(-∞,- )和(
)和( ,+∞)上的函数值大于零,g(x)=x2-2在(
,+∞)上的函数值大于零,g(x)=x2-2在( -,
-, )上函数值小于零.
)上函数值小于零.
函数 单调递增区间为(-∞,-
单调递增区间为(-∞,- ),(
),( ,+∞) --5分
,+∞) --5分
(Ⅱ)①当 <
< ≤2时,
≤2时,
∵由(Ⅰ)得 在 [0,
在 [0, ]上递减,
]上递减, 在(
在( ,
, )上递增,且
)上递增,且 =
= =0,
=0,
∴ 在[0,
在[0, ]上的最大值为
]上的最大值为 =0,
=0,
 在区间[0,
在区间[0, ]上的最小值为
]上的最小值为 =(2-2
=(2-2 )e
)e .
.
------------8分
② 当 时,
时,
∵由(Ⅰ)得 在[0,
在[0, ]上递减,
]上递减, 在(
在( ,
, )上递增,且
)上递增,且 >
> ,
,
∴ 在[0,
在[0, ]上的最大值为
]上的最大值为 =(a2-2a)ea,
=(a2-2a)ea,
 在区间[0,
在区间[0, ]上的最小值为
]上的最小值为 =(2-2
=(2-2 )e
)e .
.
------------10分
(III) 实数k的取值范围是(0,(2+2 )e
)e )
)
------------12分
【解析】略

练习册系列答案
相关题目