题目内容
6.已知x,y∈R,向量$\overrightarrow{α}$=$[\begin{array}{l}{1}\\{-1}\end{array}]$是矩阵$[\begin{array}{l}{x}&{1}\\{y}&{0}\end{array}]$的属于特征值-2的一个特征向量,求矩阵A以及它的另一个特征值.分析 利用A$\overrightarrow{α}$=-2$\overrightarrow{α}$,可得A=$[\begin{array}{l}{-1}&{1}\\{2}&{0}\end{array}]$,通过令矩阵A的特征多项式为0即得结论.
解答 解:由已知,可得A$\overrightarrow{α}$=-2$\overrightarrow{α}$,即$[\begin{array}{l}{x}&{1}\\{y}&{0}\end{array}]$ $[\begin{array}{l}{1}\\{-1}\end{array}]$=$[\begin{array}{l}{x-1}\\{y}\end{array}]$=$[\begin{array}{l}{-2}\\{2}\end{array}]$,
则$\left\{\begin{array}{l}{x-1=-2}\\{y=2}\end{array}\right.$,即$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$,
∴矩阵A=$[\begin{array}{l}{-1}&{1}\\{2}&{0}\end{array}]$,
从而矩阵A的特征多项式f(λ)=(λ+2)(λ-1),
∴矩阵A的另一个特征值为1.
点评 本题考查求矩阵及其特征值,注意解题方法的积累,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.投篮测试中,每人投3次,至少投中2次才能通过测试.己知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )
| A. | 0.648 | B. | 0.432 | C. | 0.36 | D. | 0.312 |
16.“x=1”是“x2-2x+1=0”的( )
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
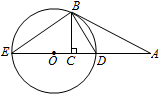 如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.
如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.