题目内容

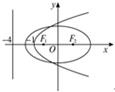精英家教网椭圆C1：
x2
4
+
y2
3
=1的左准线为l，左、右焦点分别为F1、F2，抛物线C2的准线为l，焦点为F2，C1与C2的一个交点为P，则|PF2|的值等于（　　）
A、
2
3
B、
4
3
C、2
D、
8
3
分析：P到椭圆的左准线的距离设为d，先利用椭圆的第二定义求得PF1|=
1
2
d，利用抛物线的定义可知|PF2|=d，最后根据椭圆的定义可知
|PF2|+|PF1|=4求得d，则|PF2|可得．
解答：解：椭圆的离心率为
1
2
，P到椭圆的左准线的距离设为d，则|PF1|=
1
2
d，|PF2|+|PF1|=4，又|PF2|=d，
∴d=|PF2|=
8
3
．
故选D．
点评：本题主要考查了椭圆的简单性质．解题的关键是灵活利用椭圆和抛物线的定义．
练习册系列答案
相关题目
已知椭圆C1：
x2
4
+
y2
3
=1，抛物线C2：（y-m）2=2px（p＞0），且C1、C2的公共弦AB过椭圆C1的右焦点．
（Ⅰ）当AB⊥x轴时，求m、p的值，并判断抛物线C2的焦点是否在直线AB上；
（Ⅱ）是否存在m、p的值，使抛物线C2的焦点恰在直线AB上？若存在，求出符合条件的m、p的值；若不存在，请说明理由．
已知椭圆C1：
x2
4
+y2=1，双曲线C2：
x2
3
-y2=1．若直线l：y=kx+
2
与椭圆C1、双曲线C2都恒有两个不同的交点，且l与C2的两交点A、B满足
OA
•
OB
＜6（其中O为原点），求k的取值范围．
（2012•杨浦区二模）如图，椭圆C1：
x2
4
+y2=1，x轴被曲线C2：y=x2-b截得的线段长等于C1的长半轴长．
（1）求实数b的值；
（2）设C2与y轴的交点为M，过坐标原点O的直线l与C2相交于点A、B，直线MA、MB分别与C1相交与D、E．
①证明：MD•ME=0；
②记△MAB，△MDE的面积分别是S1，S2．若
S1
S2
=λ，求λ的取值范围．
已知椭圆C1：
x2
4
+
y2
3
=1，抛物线C2：（y-m）2=2px（p＞0），且C1、C2的公共弦AB过椭圆C1的右焦点．
（1）当AB⊥x轴时，求p，m的值，并判断抛物线C2的焦点是否在直线AB上；
（2）若p=
4
3
且抛物线C2的焦点在直线AB上，求m的值及直线AB的方程．
（2013•唐山一模）已知椭圆C1：
x24
+y2=1和动圆C2：x2+y2=r2(r＞0)，直线l：y=kx+m与C1和C2分别有唯一的公共点A和B．
（I）求r的取值范围；
（II ）求|AB|的最大值，并求此时圆C2的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网