题目内容
若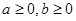 ,且当
,且当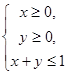 时,恒有
时,恒有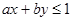 ,则以
,则以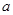 ,b为坐标点P(
,b为坐标点P(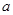 ,b)所形成的平面区域的面积等于_______
,b)所形成的平面区域的面积等于_______
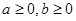 ,且当
,且当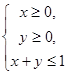 时,恒有
时,恒有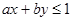 ,则以
,则以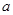 ,b为坐标点P(
,b为坐标点P(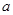 ,b)所形成的平面区域的面积等于_______
,b)所形成的平面区域的面积等于_______1
试题分析:解:令z=ax+by,∵
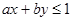 恒成立,
恒成立,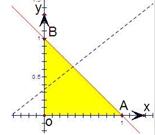
即函数z=ax+by在可行域要求的条件下,zmax≤1恒成立.当直线ax+by-z=0过点(1,0)或点(0,1)时,0≤a≤1,0≤b≤1.点P(a,b)形成的图形是边长为1的正方形.∴所求的面积S=12=1.故答案为:1
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
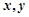 满足约束条件
满足约束条件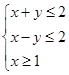 ,且
,且 恒成立,则
恒成立,则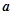 的取值范围为 。
的取值范围为 。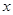 ,
,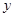 满足约束条件
满足约束条件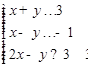 , 则目标函数
, 则目标函数 的最小值为______.
的最小值为______.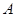 为不等式组
为不等式组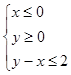 表示的平面区域,当
表示的平面区域,当 从
从 连续变化到
连续变化到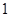 时,动直线
时,动直线 扫过
扫过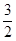
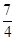

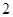
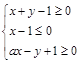 (
(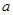 为常数)所表示的平面区域的面积等于
为常数)所表示的平面区域的面积等于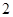 ,则
,则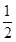

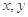 满足约束条件
满足约束条件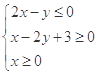 ,则目标函数
,则目标函数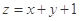 的最大值为 .
的最大值为 .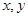 满足
满足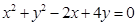 ,则
,则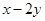 的最大值为 。
的最大值为 。