题目内容
15.已知奇函数f(x)的定义域为R,若f(x+1)为偶函数,且f(1)=1,则f(2014)+f(2015)=( )| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
分析 根据f(x)和f(x+1)的奇偶性便可得到f(x)=f(x-1+1)=f(x-4),从而得出f(x)是周期为4的周期函数,而可以求出f(2)=0,从而可以得出f(2014)+f(2015)=f(2)-f(1)=-1.
解答 解:f(x)为R上的奇函数,f(x+1)为偶函数;
∴f(x)=f(x-1+1)=f(-x+2)=-f(x-2)=f(x-4);
∴f(x)是周期为4的周期函数;
∴f(2014)+f(2015)=f(2+503×4)+f(-1+504×4)=f(2)-f(1)=f(2)-1;
f(-1+1)=f(1+1)=0;
即f(2)=0;
∴f(2014)+f(2015)=0-1=-1.
故选:B.
点评 考查奇函数、偶函数的定义,以及周期函数的定义,清楚偶函数的定义:f(-x)=f(x),是自变量换上-x后函数值不变.

练习册系列答案
相关题目
6.不等式组$\left\{{\begin{array}{l}{x≥1}\\{y≥1}\\{x+y≤4}\end{array}}\right.$,所表示的平面区域的面积为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
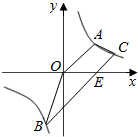 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.