��Ŀ����
����С������12�֣�
��֪��![]() ������
������![]() ��������
��������![]()
![]() ������
������![]() ���е�
���е�![]() �ڵڶ����ޣ���ͼ��
�ڵڶ����ޣ���ͼ��
 �������е�
�������е�![]() �������ꣻ
�������ꣻ
������������Ϊ![]() ����Բ
����Բ![]() ǡ�þ����е�
ǡ�þ����е�![]() ��������
��������![]() ����Բ����һ��Ϊ
����Բ����һ��Ϊ![]() ��������
��������![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ![]() ����
����![]() ������Բ���̣�
������Բ���̣�
21����С������12�֣�
��֪����![]() .
.
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ʱ��
ʱ��![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��֤����![]()
![]() .
.
22��ѡ��4��1������֤��ѡ��
��ͼ��![]() ��Բ
��Բ![]() ��ֱ����
��ֱ����![]() ���ң�
���ң�![]() ��ƽ����
��ƽ����![]() ��Բ
��Բ![]() �ڵ�
�ڵ�![]() ��
��![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
 ��1����֤��
��1����֤��![]() ��Բ
��Բ![]() �����ߣ�
�����ߣ�
��2����![]() ����
����![]() ��ֵ��
��ֵ��
23.ѡ��4��4������ϵ���������
��ƽ��ֱ������ϵ�У�ֱ��![]() ����
����![]() ����б��Ϊ
����б��Ϊ![]() ��������ԭ��Ϊ���㣬
��������ԭ��Ϊ���㣬![]() ��ķǸ�����Ϊ���ᣬ����������ϵ������
��ķǸ�����Ϊ���ᣬ����������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��ֱ��
��ֱ��![]() ������
������![]() �ཻ��
�ཻ��![]() ���㣻
���㣻
��1����![]() ����ֱ��
����ֱ��![]() ����б��
����б��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2������![]() ���ʱֱ��
���ʱֱ��![]() �IJ������̡�
�IJ������̡�
24�� ѡ��4-5 ����ʽѡ��
��֪����![]()
��I������![]() ��ֵ��
��ֵ��
��II����![]() ������
������![]() ������
������![]() ����������ʵ��a��ȡֵ��Χ��
����������ʵ��a��ȡֵ��Χ��
�⣺(��)���е�![]() ����
����![]() ��
��
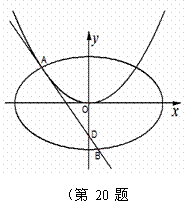 ������
������![]() ��б��Ϊ
��б��Ϊ![]() ����
����![]() �ķ���Ϊ
�ķ���Ϊ![]() ���ֵ�
���ֵ�![]() ��
��![]() �ϣ�
�ϣ�
![]() ������
������![]() ��������
��������![]()
![]() ��
��
(��)��(��) ��![]() �������
�������![]() ��
��
��![]() �����߷���Ϊ
�����߷���Ϊ![]() ����
����![]() ����
����![]() ��������Բ����Ϊ
��������Բ����Ϊ![]() ���ҹ�
���ҹ�![]() ��
��![]()
��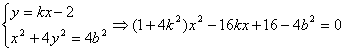 ��
��
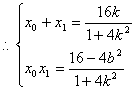 ��
��
![]()
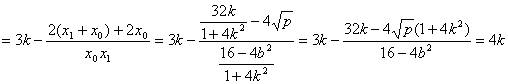
��![]() ��
��![]() ����ã�
����ã�![]() ������
������![]() ��
��
��Բ����Ϊ![]() ��
��
21���⣺��1��![]() �Ķ�����Ϊ��0��+�ޣ���
�Ķ�����Ϊ��0��+�ޣ���![]()
��![]() ʱ��
ʱ��![]() ��0����
��0����![]() �ڣ�0��+�ޣ�����������
�ڣ�0��+�ޣ�����������
��![]() ʱ��
ʱ��![]() ��0����
��0����![]() �ڣ�0��+�ޣ������ݼ���
�ڣ�0��+�ޣ������ݼ���
��-1��![]() ��0ʱ����
��0ʱ����![]() =0�����
=0�����![]() .
.
��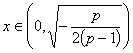 ʱ��
ʱ��![]() ��0��
��0��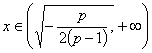 ʱ��
ʱ��![]() ��0.
��0.
��![]() ��
��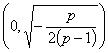 ������������
������������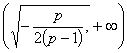 �����ݼ�
�����ݼ�
��2����Ϊ![]() ������
������
��![]() ʱ��
ʱ��![]() �����
�����![]()
��![]() ����
����![]() ,
,
��Ϊ![]() ����
����![]() ��
��![]() ��
��
�ҵ�![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() .
.
����![]() ��
��![]() �ϵ�������
�ϵ�������![]() �ϵݼ�.����
�ϵݼ�.����![]() ����
����![]()
��3���ɣ�2��֪��![]() ʱ����
ʱ����![]() ����
����![]() ʱ��
ʱ��![]() ��
��![]() ��
��
��![]() ����
����![]() ����
����![]()
����![]() ��
��![]() ������
������![]() ��
��
��ӵ�![]()
��![]()
����![]() ��
��![]()
22��ѡ��4��1������֤��ѡ��
22.��1������![]() ���ɵ�
���ɵ�![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
��![]() Ϊ�뾶����
Ϊ�뾶����![]() ��Բ
��Բ![]() ������
������
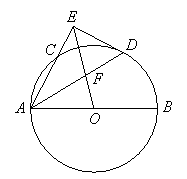 ��2����
��2����![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
����![]() ��
��
![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
��![]() �ɵ�
�ɵ�![]() ��
��
����![]() ���ɵ�
���ɵ�![]() ��
��
23.ѡ��4��4������ϵ���������
��1��������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]()
������![]() ��ֱ�Ƿ���Ϊ
��ֱ�Ƿ���Ϊ![]()
��Բ��![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() ��
��![]() ��
��![]()
��ֱ��б�ʲ�����ʱ��![]() ��������
��������
��ֱ��б�ʴ���ʱ����![]() ��
��![]()
��![]() ��������5�� ��ֱ����б�ǵ�ȡֵ��Χ��
��������5�� ��ֱ����б�ǵ�ȡֵ��Χ��![]()
��2��Ҫʹ��![]() ��̣�ֻ��
��̣�ֻ��![]() ����ֱ��
����ֱ��![]() ����б��Ϊ
����б��Ϊ![]() ��
��
��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ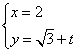 ��
��![]() ������
������
24�� ѡ��4-5 ����ʽѡ��
�⣺��I��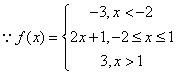 ��
��![]() ��
��
��II����![]()
![]() �����ҽ���
�����ҽ���![]() ʱȡ�õȺš����ɣ�I��֪
ʱȡ�õȺš����ɣ�I��֪![]() �����ֵΪ3.
�����ֵΪ3.
����![]() ������
������![]() ��������
��������
![]() ����֮��
����֮��![]() ��
��
��ʵ��a��ȡֵ��Χ��![]()

 ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�