Question

（本小题满分12分）已知命题p：函数在内有且仅有一个零点．命题q：在区间内恒成立．若命题“p且q”是假命题，求实数的取值范围．

Answer 1

{A| 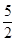－ <A≤－1或A≥1}

解析试题分析：先考查命题p：
若A＝0，则容易验证不合题意；
故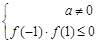，解得：A≤－1或A≥1.
再考查命题q：
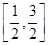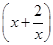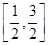∵x∈，∴3(A+1)≤－在上恒成立．
易知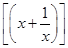 _mAx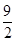＝，故只需3(A+1) ≤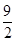－即可．解得A≤－.  
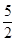∵命题“p且q”是假命题，∴命题p和命题q中一真一假。
当p真q假时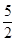，－ <A≤－1或A≥1；
当p假q真时，．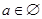
综上，A的取值范围为{A| 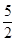－ <A≤－1或A≥1}
考点：复合命题；二次函数的性质；函数的零点；二次方程根的分布问题。
点评：当一元二次方程有两相等实根时，此时对应的二次函数叫做有一个零点，而不是两个零点。我们一定要注意这一条，做题时容易出错。