题目内容
已知函数f(x)=x|x+2|-2x-1
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)写出函数的单调区间.
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)写出函数的单调区间.
分析:(1)根据绝对值的定义,分x≥-2与x<-2两种情况加以讨论,分别化简函数的表达式,再综上所述即可得到函数f(x)用分段函数的形式表示的式子;
(2)根据f(x)用分段函数的形式表示的式子,可得它的图象是由两个二次函数的图象各取一部分拼接而成,由此结合二次函数的图象作法,即可作出函数y=f(x)的图象;
(3)由(2)作出的图象加以观察,即可写出函数y=f(x)的单调区间.
(2)根据f(x)用分段函数的形式表示的式子,可得它的图象是由两个二次函数的图象各取一部分拼接而成,由此结合二次函数的图象作法,即可作出函数y=f(x)的图象;
(3)由(2)作出的图象加以观察,即可写出函数y=f(x)的单调区间.
解答:解:(1)∵当x≥-2时,f(x)=x|x+2|-2x-1=x(x+2)-2x-1=x2-1;
当x<-2时,f(x)=x|x+2|-2x-1=x(-x-2)-2x-1=-x2-4x-1
∴函数用分段函数的形式表示为f(x)=
…(4分)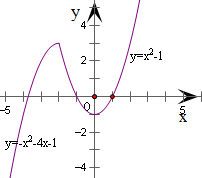
(2)∵当x≥-2时,f(x)=x2-1,
函数图象是抛物线y=x2-1位于直线x=-2右侧部分;
当x<-2时,f(x)=-x2-4x-1,
函数图象是抛物线y=-x2-4x-1位于直线x=-2左侧部分
∴函数y=f(x)图象由抛物线y=x2-1位于x=-2右侧部分与抛物线
y=-x2-4x-1位于x=-2左侧部分拼接而成,
因此作出函数y=f(x)图象,如图右图所示…(10分)
(3)由(2)所作的函数图象,可得
函数f(x)的单调增区间是(-∞,-2)和(0,+∞)
单调减区间是(-2,0)…(14分)
当x<-2时,f(x)=x|x+2|-2x-1=x(-x-2)-2x-1=-x2-4x-1
∴函数用分段函数的形式表示为f(x)=
|

(2)∵当x≥-2时,f(x)=x2-1,
函数图象是抛物线y=x2-1位于直线x=-2右侧部分;
当x<-2时,f(x)=-x2-4x-1,
函数图象是抛物线y=-x2-4x-1位于直线x=-2左侧部分
∴函数y=f(x)图象由抛物线y=x2-1位于x=-2右侧部分与抛物线
y=-x2-4x-1位于x=-2左侧部分拼接而成,
因此作出函数y=f(x)图象,如图右图所示…(10分)
(3)由(2)所作的函数图象,可得
函数f(x)的单调增区间是(-∞,-2)和(0,+∞)
单调减区间是(-2,0)…(14分)
点评:本题给出含有绝对值符号的函数,求作函数的图象并写出函数的单调区间,着重考查了绝对值的意义、函数的单调性和二次函数的图象与性质等知识,属于中档题.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|