题目内容
已知抛物线![]() 的焦点为F,过点F作直线
的焦点为F,过点F作直线![]() 与抛物线交于A,B两点,抛物线的准线与
与抛物线交于A,B两点,抛物线的准线与![]() 轴交于点C。
轴交于点C。
(1)证明:![]() ;
;
(2)求![]() 的最大值,并求
的最大值,并求![]() 取得最大值时线段AB的长。
取得最大值时线段AB的长。
解:
(Ⅰ)由题设知,F(![]() ,0),C(-
,0),C(-![]() ,0),
,0),
设A(x1,y1),B(x2,y2),直线l方程为x=my+![]() ,
,
代入抛物线方程y2=2px,得y2-2pmy-p2=0.
y1+y2=2pm,y1y2=-p2. …4分
不妨设y1>0,y2<0,则
tan∠ACF=![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
tan∠BCF=-![]() =-
=-![]() ,
,
∴tan∠ACF=tan∠BCF,所以∠ACF=∠BCF. …8分
(Ⅱ)如(Ⅰ)所设y1>0,tan∠ACF=![]() ≤
≤![]() =1,当且仅当y1=p时取等号,
=1,当且仅当y1=p时取等号,
此时∠ACF取最大值![]() ,∠ACB=2∠ACF取最大值
,∠ACB=2∠ACF取最大值![]() ,
,
并且A(![]() ,p),B(
,p),B(![]() ,-p),|AB|=2p. …12分
,-p),|AB|=2p. …12分

练习册系列答案
相关题目
 的焦点为F,过F的直线交抛物线于M、N两点,其准线
的焦点为F,过F的直线交抛物线于M、N两点,其准线 与x轴交于K点.
与x轴交于K点.
 的最小值.
的最小值. 的焦点为F,过抛物线在第一象限部分上一点P的切线为
的焦点为F,过抛物线在第一象限部分上一点P的切线为 ,过P点作平行于
,过P点作平行于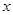 轴的直线
轴的直线 ,过焦点F作平行于
,过焦点F作平行于 ,则点P的坐标为 。
,则点P的坐标为 。 的焦点为F,过点F作直线
的焦点为F,过点F作直线 与抛物线交于A,B两点,抛物线的准线与
与抛物线交于A,B两点,抛物线的准线与 轴交于点C。
轴交于点C。 ;
; 的最大值,并求
的最大值,并求 的焦点为F,过点
的焦点为F,过点 的直线
的直线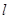 与
与 相交于
相交于 、
、 两点,点A关于
两点,点A关于 轴的对称点为D .
轴的对称点为D . ,求
,求 的内切圆M的方程 .
的内切圆M的方程 . 的焦点为F,准线为
的焦点为F,准线为 ,经过F且斜率为
,经过F且斜率为 的直线与抛物线在
的直线与抛物线在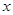 轴上方的部分相交于点A,且AK
轴上方的部分相交于点A,且AK
 的面积是( )
的面积是( ) C
C  D 8
D 8