Question

（本小题满分12分）已知，如图，AB是⊙O的直径，G为AB延长线上的一点，GCD是⊙O的割线，过点G作AB的垂线，交直线AC于点E，交AD于点F，过G作⊙O的切线，切点为H.

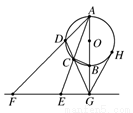
求证：(1)C，D，F，E四点共圆；

(2)GH²＝GE·GF.

 

 

Answer 1

【答案】

见解析。

【解析】本题考查的知识点是与圆相关的比例线段及圆内接四边形的判定，其中根据圆内接四边形判定定理，判断C，D，F，E四点共圆，是解答本题的关键．

（I）连接BC．由已知中AB是⊙O的直径，可得∠ACB=90°，由过点G作AB的垂线，交AC的延长线于点E，可得∠AGE=90°，进而得到∠FDC=∠AEG，根据圆内接四边形判定定理，即可得到C，D，F，E四点共圆；

（Ⅱ）由（I）中C，D，F，E四点共圆，则GCD和GEF分别为圆的两条件割线，则GE•GF=GC•GD，又由已知中GH为圆O的切线，GCD为圆O的割线，由切割线定理可得GH²=GC•GD，进而得到结论．

证明：(1)连接CB，

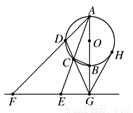
∵∠ACB＝90°，AG⊥FG，

又∵∠EAG＝∠BAC，

∴∠ABC＝∠AEG.

∵∠ADC＝180°－∠ABC

＝180°－∠AEG＝∠CEF，

∴∠ADC＋∠FDC＝∠CEF＋∠FDC＝180°，

∴C，D，F，E四点共圆．                       …………6分

(2)由C，D，F，E四点共圆，知∠GCE＝∠AFE，∠GEC＝∠GDF，

∴△GCE∽△GFD，

故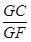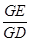＝，即GC·GD＝GE·GF.

∵GH为圆的切线，GCD为割线，

∴GH²＝GC·GD，∴GH2＝GE·GF.                   …………12分