题目内容
 在三棱柱ABC-A′B′C′中,侧面CBB′C′⊥底面ABC,∠B′BC=60°,
在三棱柱ABC-A′B′C′中,侧面CBB′C′⊥底面ABC,∠B′BC=60°,∠ACB=90°,且CB=CC′=CA.
(1)求证:平面AB′C⊥平面A′C′B;
(2)求异面直线A′B与AC′所成的角.
分析:(1)由已知中三棱柱ABC-A′B′C′中,侧面CBB′C′⊥底面ABC,∠ACB=90°,由面面垂直的性质可得AC⊥平面CBB′C′,进而得到AC⊥BC′,又由CB=C′C′,我们可以得到四边形BCC′B′为菱形,进而得到BC′⊥B′C,然后根据线面垂直的判定定理及面面垂直的判定定理得到平面AB′C⊥平面A′C′B;
(2)延长CA到D,使CA=AD,连A'D,BD.根据棱柱的结构特征,结合异面直线夹角的定义,易得到∠DA′B为异面直线A'B与AC'所成的角,解三角形∠DA′B,即可得到异面直线A′B与AC′所成的角.
(2)延长CA到D,使CA=AD,连A'D,BD.根据棱柱的结构特征,结合异面直线夹角的定义,易得到∠DA′B为异面直线A'B与AC'所成的角,解三角形∠DA′B,即可得到异面直线A′B与AC′所成的角.
解答: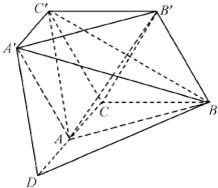 解:(1)∵平面CBB'C'⊥平面ABC,AC⊥BC,
解:(1)∵平面CBB'C'⊥平面ABC,AC⊥BC,
AC⊥平面CBB′C′,
∴AC⊥BC′.(2分)
∵在平行四边形BCC′B′中,CB=C′C′,∴平行四边形BCC′B′为菱形.
∴BC′⊥B′C
∴BC′⊥平面AB'C. (4分)
又BC'?平面A′C′B
∴平面AB'C⊥平面A'C'B.(6分)
(2)延长CA到D,使CA=AD,连A'D,BD.
∵AC∥A′C′,AC=A′C′,∴AD∥A′C′,AD=A′C′.
∴ADA′C′为平行四边形.
∴A′D∥AC′,A′D=AC′,
∴∠DA′B为异面直线A'B与AC'所成的角. (9分)
设BC=a,∴∠BCD=90°BC=aCD=2a,
∴BD=
=
a
∴AC⊥平在菱形BCC'B',∠CBB'=60°,BC=a,
又∵A′D=A′C=
a从而在三角形AB′D中,cosDA′B=
=
.
∴∠DA′B=arccos
(11分)
∴异面直线A'B与AC'所成的角的大小为arccos
. (12分)
 解:(1)∵平面CBB'C'⊥平面ABC,AC⊥BC,
解:(1)∵平面CBB'C'⊥平面ABC,AC⊥BC,AC⊥平面CBB′C′,
∴AC⊥BC′.(2分)
∵在平行四边形BCC′B′中,CB=C′C′,∴平行四边形BCC′B′为菱形.
∴BC′⊥B′C
∴BC′⊥平面AB'C. (4分)
又BC'?平面A′C′B
∴平面AB'C⊥平面A'C'B.(6分)
(2)延长CA到D,使CA=AD,连A'D,BD.
∵AC∥A′C′,AC=A′C′,∴AD∥A′C′,AD=A′C′.
∴ADA′C′为平行四边形.
∴A′D∥AC′,A′D=AC′,
∴∠DA′B为异面直线A'B与AC'所成的角. (9分)
设BC=a,∴∠BCD=90°BC=aCD=2a,
∴BD=
| BC2+CD2 |
| 5 |
∴AC⊥平在菱形BCC'B',∠CBB'=60°,BC=a,
又∵A′D=A′C=
| 2 |
| A′D2+A′B2-BD2 |
| 2A′D×A′B |
| ||
| 8 |
∴∠DA′B=arccos
| ||
| 8 |
∴异面直线A'B与AC'所成的角的大小为arccos
| ||
| 8 |
点评:本题考查的知识点是平面与平面垂直的判定,及异面直线所成的角,其中(1)中熟练掌握空间线面、线线、面面垂直之间的转化是关键,(2)中找出与异面直线A′B与AC′所成的角相等的平面角是关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )| A、3:2 | B、7:5 | C、8:5 | D、9:5 |
 10、如图,在三棱柱ABC-A′B′C′中,点E、F、H、K分别为AC′、CB′、A′B、B′C′的中点,G为△ABC的重心从K、H、G、B′中取一点作为P,使得该棱柱恰有2条棱与平面PEF平行,则P为( )
10、如图,在三棱柱ABC-A′B′C′中,点E、F、H、K分别为AC′、CB′、A′B、B′C′的中点,G为△ABC的重心从K、H、G、B′中取一点作为P,使得该棱柱恰有2条棱与平面PEF平行,则P为( ) 如图,在三棱柱ABC-A'B'C'中,点D是BC的中点,欲过点A'作一截面与平面AC'D平行,问应当怎样画线,并说明理由.
如图,在三棱柱ABC-A'B'C'中,点D是BC的中点,欲过点A'作一截面与平面AC'D平行,问应当怎样画线,并说明理由.