题目内容
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为 ,则a的值为 .
,则a的值为 .

 ,则a的值为 .
,则a的值为 .
-1
f'(x)=-3x2+2ax+b,∵f'(0)=0,∴b=0,
∴f(x)=-x3+ax2,令f(x)=0,得x=0或x=a(a<0).
S阴影=-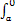 (-x3+ax2)dx=
(-x3+ax2)dx= a4=
a4= ,∴a=-1.
,∴a=-1.
∴f(x)=-x3+ax2,令f(x)=0,得x=0或x=a(a<0).
S阴影=-
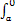 (-x3+ax2)dx=
(-x3+ax2)dx= a4=
a4= ,∴a=-1.
,∴a=-1.
练习册系列答案
相关题目
 ,则函数
,则函数 的图象的一条对称轴方程为( )
的图象的一条对称轴方程为( )



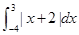 (2)
(2)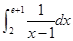
 与直线
与直线 围成的封闭区域为M,则区域M的面积为( )
围成的封闭区域为M,则区域M的面积为( )

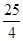
 f(x)dx=1,
f(x)dx=1, f(x)dx=-1,则
f(x)dx=-1,则 f(x)dx=________.
f(x)dx=________. 所围成的平面区域的面积为( )
所围成的平面区域的面积为( ) (sinx-cosx)dx
(sinx-cosx)dx (sinx-cosx)dx
(sinx-cosx)dx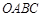 内:记抛物线
内:记抛物线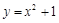 与直线
与直线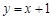 围成的区域为
围成的区域为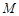 (图中阴影部分).随机往矩形
(图中阴影部分).随机往矩形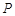 ,则点
,则点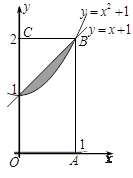




 dx=________.
dx=________. 则
则 的大小关系为( )
的大小关系为( )

