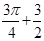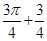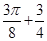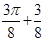题目内容
设第一象限内的点(x,y)满足约束条件 , 若目标函数z=ax+by(a>0,b>0)的最大值为40,则
, 若目标函数z=ax+by(a>0,b>0)的最大值为40,则 的最小值为( )
的最小值为( )
 , 若目标函数z=ax+by(a>0,b>0)的最大值为40,则
, 若目标函数z=ax+by(a>0,b>0)的最大值为40,则 的最小值为( )
的最小值为( ) A. | B.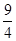 | C.1 | D.4 |
B
因为不等式表示的平面区域阴影部分,
当直线ax+by=z(a>0,b>0)过直线x-y+2=0与直线2x-y-6=0的交点(8,10)时,
目标函数z=ax+by(a>0,b>0)取得最大40,
即8a+10b=40,即4a+5b=20,那么利用均值不等式可知函数的最值为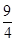 ,选B
,选B
当直线ax+by=z(a>0,b>0)过直线x-y+2=0与直线2x-y-6=0的交点(8,10)时,
目标函数z=ax+by(a>0,b>0)取得最大40,
即8a+10b=40,即4a+5b=20,那么利用均值不等式可知函数的最值为
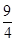 ,选B
,选B
练习册系列答案
相关题目
 满足约束条件
满足约束条件 ,目标函数
,目标函数 的最小值是 。
的最小值是 。
 满足
满足 ,则
,则 的最小值为( )
的最小值为( )



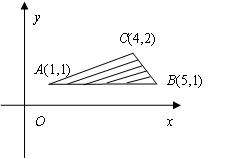
 表示的平面区域内的点为( )
表示的平面区域内的点为( )



 元/分钟和200元/分钟,甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?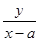 的最大值是 ( )
的最大值是 ( )
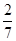
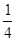
 满足约束条件
满足约束条件 若目标函数
若目标函数 的值是最大值为12,则
的值是最大值为12,则 的最小值为( ).
的最小值为( ). 


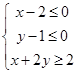 所表示的平面区域的面积是
所表示的平面区域的面积是 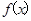 为奇函数,
为奇函数,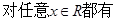
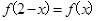 ,当
,当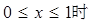
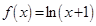 .若
.若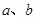 为正的常数,且对任意实数
为正的常数,且对任意实数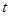 ,函数
,函数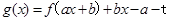 只有一个零点,当
只有一个零点,当 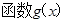 的零点
的零点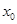 满足
满足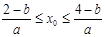 ,则点(
,则点(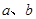 )形成的平面区域的面积为( )
)形成的平面区域的面积为( )