题目内容
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有Ⅳ人参加,现将所有参加者按年龄情况分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
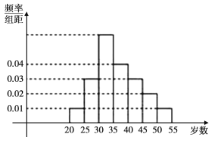
,![]() 等七组,其频率分布直方图如图所示,已知
等七组,其频率分布直方图如图所示,已知![]() 这组的参加者是6人.
这组的参加者是6人.
(1)已知![]() 和
和![]() 这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中恰有1名数学老师的概率;
这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中恰有1名数学老师的概率;
(2)组织者从![]() 这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为
这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为![]() ,求
,求![]() 的分布列和均值.
的分布列和均值.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据频率分布直方图,先得到年龄在![]() 之间的概率,再由
之间的概率,再由![]() 这组的参加者是6人,求得参加的总人数.然后分别求得年龄在
这组的参加者是6人,求得参加的总人数.然后分别求得年龄在![]() 和
和![]() 之间的人数,然后利用古典概型的概率求解.
之间的人数,然后利用古典概型的概率求解.
(2)先得到年龄在![]() 的人数,根据有4名女教师,则
的人数,根据有4名女教师,则![]() 的可能取值为:1,2,3,然后求得相应的概率,列出分布列再求期望.
的可能取值为:1,2,3,然后求得相应的概率,列出分布列再求期望.
(1)因为年龄在![]() 之间的概率为
之间的概率为![]() ,
,
又![]() 这组的参加者是6人,
这组的参加者是6人,
所以参加的总人数为![]() ,
,
所以年龄在![]() 之间的人数为
之间的人数为![]() ,
,
年龄在![]() 之间的人数为
之间的人数为![]() ,
,
所以两组选出的人中恰有1名数学老师的概率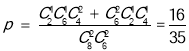 .
.
(2)年龄在![]() 的人数为:
的人数为:![]() ,从中随机选取3名担任后勤保障工作,其中女教师的人数为
,从中随机选取3名担任后勤保障工作,其中女教师的人数为![]() ,
,![]() 的可能取值为:1,2,3
的可能取值为:1,2,3
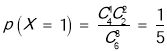
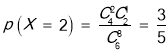

分布列为:
X | 1 | 2 | 3 |
p |
|
|
|
均值![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目



