题目内容
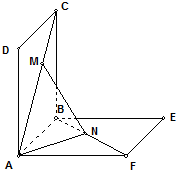 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<| 2 |
(1)求MN的长;
(2)a为何值时,MN的长最小;
(3)当MN的长最小时,求面MNA与面MNB所成二面角α的大小.
分析:(1)作MP∥AB交BC于点,NQ∥AB交BE于点Q,连接PQ,易证MNQP是平行四边形,根据MN=PQ=
即可求出MN的长;
(2)根据(1)将MN 关于a的函数进行配方即可求出MN的最小值,注意取最小值时a的取值;
(3)取MN的中点G,连接AG、BG,根据二面角的平面角的定义可知∠AGB即为二面角的平面角,在三角形AGB中利用余弦定理求出此角的余弦值,结合图形可二面角与之互补.
| (1-CP)2+BQ2 |
(2)根据(1)将MN 关于a的函数进行配方即可求出MN的最小值,注意取最小值时a的取值;
(3)取MN的中点G,连接AG、BG,根据二面角的平面角的定义可知∠AGB即为二面角的平面角,在三角形AGB中利用余弦定理求出此角的余弦值,结合图形可二面角与之互补.
解答:解(1)作MP∥AB交BC于点,NQ∥AB交BE于点Q,连接PQ,依题意可得MP∥NQ,且MP=NQ,即MNQP是平行四边形.
∴MN=PQ
由已知CM=BN=a,CB=AB=BE=1
∴AC=BF=
,CP=BQ=
a
MN=PQ=
=
=
=
(0<a<
)
(2)由(1)
MN=PQ=
=
=
=
(0<a<
)
所以,当时,MN=
即当M、N分别为AC、BF的中点时,MN的长最小,最小值为
(3)取MN的中点G,连接AG、BG,
∵AM=AN,BM=BN,G为的中点
∴AG⊥MN,BG⊥MN,即∠AGB即为二面角的平面角α
又AG=BG=
,所以,由余弦定理有cosα=
=-
故所求二面角为:α=π-arccos
∴MN=PQ
由已知CM=BN=a,CB=AB=BE=1
∴AC=BF=
| 2 |
| ||
| 2 |
MN=PQ=
| (1-CP)2+BQ2 |
=
(1-
|
=
(a-
|
| 2 |
(2)由(1)
MN=PQ=
| (1-CP)2+BQ2 |
=
(1-
|
=
(a-
|
| 2 |
所以,当时,MN=
| ||
| 2 |
即当M、N分别为AC、BF的中点时,MN的长最小,最小值为
| ||
| 2 |
(3)取MN的中点G,连接AG、BG,
∵AM=AN,BM=BN,G为的中点
∴AG⊥MN,BG⊥MN,即∠AGB即为二面角的平面角α
又AG=BG=
| ||
| 4 |
(
| ||||||||
2•
|
| 1 |
| 3 |
故所求二面角为:α=π-arccos
| 1 |
| 3 |
点评:本题主要考查了与二面角有关的立体几何综合题,涉及到的知识点比较多,知识性技巧性都很强.

练习册系列答案
相关题目
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= 8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:
8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论: 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE. (2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
(2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为