Question

12．若三棱锥P-ABC的三条侧棱PA，PB，PC两两互相垂直且长都相等，其外接球半径为2，则三棱锥的表面积为$8+\frac{{8\sqrt{3}}}{3}$．

Answer 1

分析 把三棱锥镶嵌在正方体中，根据其外接球的半径为R=$\frac{\sqrt{3}}{2}$PA，再利用三棱锥的外接球半径为2，得出2=$\frac{\sqrt{3}}{2}$PA可知$PA=\frac{{4\sqrt{3}}}{3}$，
再利用三角形的面积公式求解即可，从而三棱锥的表面积为$8+\frac{{8\sqrt{3}}}{3}$

解答 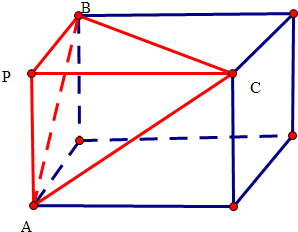解：把三棱锥P-ABC镶嵌在正方体中，如图：
根据题意得出：以PA，PB，PC为棱的正方体，PA=PB=PC，外接球的半径为R=$\frac{\sqrt{3}}{2}$PA，
∵外接球半径为R=2，
∴$PA=\frac{{4\sqrt{3}}}{3}$，AB=$\frac{4\sqrt{6}}{3}$，
∵△PAB≌△PAC≌△PBC，且为等腰直角三角形，△ABC为正三角形，
∴S_△PAB=S_△PAC=S_△PBC=$\frac{1}{2}×$（PA）²，S_△ABC=$\frac{\sqrt{3}}{4}$×（AB）²，
∴三棱锥的P-ABC的表面积为：3×$\frac{1}{2}×$（$\frac{4\sqrt{3}}{3}$）²$+\frac{\sqrt{3}}{4}$×（$\frac{4\sqrt{6}}{3}$）²=8+$\frac{8\sqrt{3}}{3}$，
故答案为：8+$\frac{8\sqrt{3}}{3}$．

点评 球的内接几何体问题是高考热点问题，本题通过求球的截面面积，对学生的空间想象能力及运算求解能力进行考查，具有一定的难度，属于中档题．