题目内容
[x]表示不超过x的最大整数,正项数列{an}满足a1=1,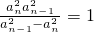 .
.
(1)求数列{an}的通项公式an;
(2)求证: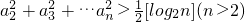 ;
;
(3)已知数列{an}的前n项和为Sn,求证:当n>2时,有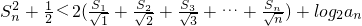 .
.
(1)解:∵
∴
∵
∴ 是以1为首项1为公差的等差数列
是以1为首项1为公差的等差数列
∴
∴ ;
;
(2)证明:
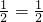 ,
, ,…,
,…,
设n-1=1+2+…+2m+k,其中k,m∈N且0≤k<2m+1
则
又2m+1≤n=2m+1+k<2m+2
从而m+1≤log2n<m+2
∴[log2n]=m+1
所以
∴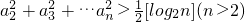 ;
;
(3)证明:∵
∴
∴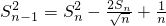
∴当n>2时,

…

累加得: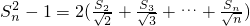 -
-
由(2)结论有
∴

=
分析:(1)根据 ,取其倒数,即可求得数列{an}的通项公式an;
,取其倒数,即可求得数列{an}的通项公式an;
(2) ,设n-1=1+2+…+2m+k,其中k,m∈N且0≤k<2m+1,则
,设n-1=1+2+…+2m+k,其中k,m∈N且0≤k<2m+1,则 ,又2m+1≤n=2m+1+k<2m+2,从而m+1≤log2n<m+2,故可得证.
,又2m+1≤n=2m+1+k<2m+2,从而m+1≤log2n<m+2,故可得证.
(3) 两边平方,并整理可得:当n>2时,
两边平方,并整理可得:当n>2时, .又
.又 ,…,
,…, ,累加得:
,累加得: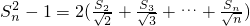 -
- ,利用(2)结论可得
,利用(2)结论可得 ,所以
,所以 ,从而问题可证.
,从而问题可证.
点评:本题以数列的递推式为载体,考查数列的通项,考查不等式的证明,考查累加法求和,同时考查新定义的理解,属于中档题

∴

∵

∴
 是以1为首项1为公差的等差数列
是以1为首项1为公差的等差数列∴

∴
 ;
;(2)证明:

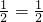 ,
, ,…,
,…,
设n-1=1+2+…+2m+k,其中k,m∈N且0≤k<2m+1
则

又2m+1≤n=2m+1+k<2m+2
从而m+1≤log2n<m+2
∴[log2n]=m+1
所以

∴
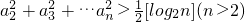 ;
;(3)证明:∵

∴

∴
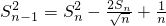
∴当n>2时,


…

累加得:
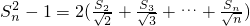 -
-
由(2)结论有

∴


=

分析:(1)根据
 ,取其倒数,即可求得数列{an}的通项公式an;
,取其倒数,即可求得数列{an}的通项公式an;(2)
 ,设n-1=1+2+…+2m+k,其中k,m∈N且0≤k<2m+1,则
,设n-1=1+2+…+2m+k,其中k,m∈N且0≤k<2m+1,则 ,又2m+1≤n=2m+1+k<2m+2,从而m+1≤log2n<m+2,故可得证.
,又2m+1≤n=2m+1+k<2m+2,从而m+1≤log2n<m+2,故可得证.(3)
 两边平方,并整理可得:当n>2时,
两边平方,并整理可得:当n>2时, .又
.又 ,…,
,…, ,累加得:
,累加得: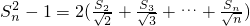 -
- ,利用(2)结论可得
,利用(2)结论可得 ,所以
,所以 ,从而问题可证.
,从而问题可证.点评:本题以数列的递推式为载体,考查数列的通项,考查不等式的证明,考查累加法求和,同时考查新定义的理解,属于中档题

练习册系列答案
相关题目