题目内容
函数 在区间
在区间 上的最小值为( )
上的最小值为( )
A. | B. | C. | D. |
D
解析试题分析:要求函数在区间 上的最小值,一般要确定函数在此区间上的单调性,这里我们利用导数的性质来解决.
上的最小值,一般要确定函数在此区间上的单调性,这里我们利用导数的性质来解决. ,易知当
,易知当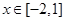 时,
时,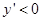 ,函数
,函数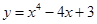 递减,当
递减,当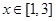 时,
时, ,函数
,函数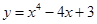 递增,因此在
递增,因此在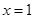 时,函数
时,函数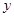 取得最小值0.
取得最小值0.
考点:函数的最值.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知函数 是偶函数,且
是偶函数,且 ,当
,当 时,
时, ,则方程
,则方程 在区间
在区间 上的解的个数是( )
上的解的个数是( )
| A.8 | B.9 | C.10 | D.11 |
若函数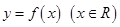 满足
满足 且
且 时,
时, ,函数
,函数 ,则函数
,则函数 在区间
在区间 内的零点的个数为 ( )
内的零点的个数为 ( )
| A.7 | B.8 | C.9 | D.10 |
下列函数中,既是偶函数又在区间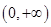 上是单调递减函数的是( )
上是单调递减函数的是( )
A.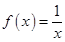 | B.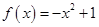 | C.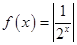 | D.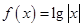 |
若关于 的两个方程
的两个方程 、
、 的解分别为
的解分别为 、
、 (其中
(其中 是大于1的常数),则
是大于1的常数),则 的值( )
的值( )
| A.大于0 | B.小于0 |
| C.等于0 | D.以上都不对,与 的值有关 的值有关 |
函数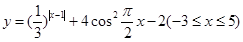 ,则此函数的所有零点之和等于( )
,则此函数的所有零点之和等于( )
| A.4 | B.8 | C.6 | D.10 |
若函数 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A. , , 在 在 上是增函数 上是增函数 |
B. , , 在 在 上是减函数 上是减函数 |
C. , , 是偶函数 是偶函数 |
D. , , 是奇函数 是奇函数 |
下列函数中与 为同一函数的是
为同一函数的是
A. | B. | C. | D.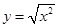 |
 时,
时, 恒成立(
恒成立( 为函数
为函数 的导函数);②对任意的
的导函数);②对任意的 都有
都有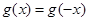 ,又函数
,又函数 满足:对任意的
满足:对任意的 成立。当
成立。当 时,
时, 。若关于
。若关于 的不等式
的不等式 对
对 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )


 或
或