题目内容
若函数f(x)=x3+ax2+bx+c有极值点x1,x2,且f(x1)=x1,则关于x的方程3(f(x))2+2af(x)+b=0的不同实数根的个数是 ( )
| A.3 | B.4 | C.5 | D.6 |
A
解析试题分析:求导得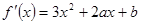 ,显然
,显然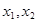 是方程
是方程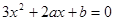 的二不等实根,不妨设
的二不等实根,不妨设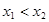 ,于是关于x的方程3(f(x))2+2af(x)+b=0的解就是
,于是关于x的方程3(f(x))2+2af(x)+b=0的解就是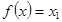 或
或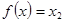 ,根据题意画图:
,根据题意画图: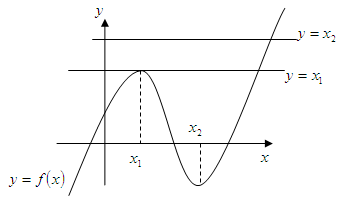
所以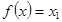 有两个不等实根,
有两个不等实根,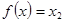 只有一个不等实根,故答案选A.
只有一个不等实根,故答案选A.
考点:导数、零点、函数的图象

练习册系列答案
相关题目
函数 ,则函数
,则函数 与
与 轴的交点个数是( )
轴的交点个数是( )
| A.1 | B.2 | C.3 | D.4 |
若方程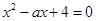 在[1,4]上有实数解,则实数
在[1,4]上有实数解,则实数 的取值范围是( )
的取值范围是( )
| A.[4,5] | B.[3,5] | C.[3,4] | D.[4,6] |
下列函数中,既是奇函数又是增函数的为( )
A. | B. | C. | D. |
下列函数为偶函数的是 ( )
A. | B. | C. | D. |
若函数f(x) (x∈R)是奇函数,函数g(x) (x∈R)是偶函数,则 ( )
A.函数f(x) g(x)是偶函数 g(x)是偶函数 | B.函数f(x) g(x)是奇函数 g(x)是奇函数 |
| C.函数f(x)+g(x)是偶函数 | D.函数f(x)+g(x)是奇函数 |
若函数 是函数
是函数 (
(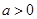 ,且
,且 )的反函数,其图象经过点
)的反函数,其图象经过点 ,则
,则 ( )
( )
A. | B. | C. | D. |
 (
( )的图象上有一点
)的图象上有一点 ,该函数的图象与x轴、直线x=-1及 x=t围成图形(如图阴影部分)的面积为S,则S与t的函数关系图可表示为( )
,该函数的图象与x轴、直线x=-1及 x=t围成图形(如图阴影部分)的面积为S,则S与t的函数关系图可表示为( )
 的图象是 ( )
的图象是 ( )
