题目内容
执行下面框图所描述的算法程序,记输出的一列数依次为a1,a2,…,an,n∈N*,n≤2011.(注:框图中的赋值符号“=”也可以写成“←”或“:=”)
(1)若输入λ=
| 2 |
(2)若输入λ=2,令bn=
| 1 |
| an-1 |
(3)若输入λ=
| 5 |
| 2 |
| 2an-1 |
| an-2 |
| 8 |
| 9 |
分析:(1)根据程序框图循环结构图直接可以判断当λ=
时的输出结果,(2)结合题干条件求证bn+1-bn是一个常数,即可求出数列an的通项公式,(3)首先证明cn是等比数列,然后根据等比数列求和公式求出Tn,最后进行大小比较.
| 2 |
解答:解:(1)输出结果为0,
,
.(4分)
(注:写对第一个数给(1分),写对二个数得(2分).)
(2)当λ=2时,bn+1-bn=
-
=
-
=
-
=-1(常数),
n∈N*,n≤2010.
所以,bn是首项b1=-1,公差d=-1的等差数列.(6分)
故bn=-n,
=-n,数列an的通项公式为an=1-
,n∈N*,n≤2011.(9分)
(3)当λ=
时,an+1=
,cn=
=
=
=
=
,(11分)
∴cn是以
为首项,
为公比的等比数列.cn=
(
)n-1=2(
)nTn=c1+2c2+3c3++n•cn=2(
)+4(
)2+6(
)3++2n(
)n
Tn=2(
)2+4(
)3+6(
)4++2n(
)n+1
两式作差得(1-
)Tn=2(
)+2(
)2+2(
)3+2(
)4++2(
)n-2n(
)n+1
即
Tn=
-2n(
)n+1=
[1-(
)n]-2n(
)n+1∴Tn=
[1-(
)n]-
(
)n+1=
-
(
)n-
(
)n+1(13分)
当n=2011时,T=
-
(
)2011-
•2011•(
)2012<
(14分)
| ||
| 2 |
| 2 |
(注:写对第一个数给(1分),写对二个数得(2分).)
(2)当λ=2时,bn+1-bn=
| 1 |
| an+1-1 |
| 1 |
| an-1 |
| 1 | ||
|
| 1 |
| an-1 |
| 2-an |
| an-1 |
| 1 |
| an-1 |
n∈N*,n≤2010.
所以,bn是首项b1=-1,公差d=-1的等差数列.(6分)
故bn=-n,
| 1 |
| an-1 |
| 1 |
| n |
(3)当λ=
| 5 |
| 2 |
| 1 | ||
|
| 2an-1 |
| an-2 |
| cn+1 |
| cn |
| ||
|
| ||||||||||
|
| ||||
|
| 1 |
| 4 |
∴cn是以
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
两式作差得(1-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
即
| 3 |
| 4 |
2•(
| ||||
1-
|
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 8 |
| 9 |
| 1 |
| 4 |
| 8n |
| 3 |
| 1 |
| 4 |
| 8 |
| 9 |
| 8 |
| 9 |
| 1 |
| 4 |
| 8n |
| 3 |
| 1 |
| 4 |
当n=2011时,T=
| 8 |
| 9 |
| 8 |
| 9 |
| 1 |
| 4 |
| 8 |
| 3 |
| 1 |
| 4 |
| 8 |
| 9 |
点评:本题主要考查程序框图和数列求和的知识点,解答本题的关键是看懂程序框图的运算程序,熟练掌握等差和等比数列的性质,本题把程序框图和数列的知识点结合在一起进行考查,也是一道不错的习题.

练习册系列答案
相关题目
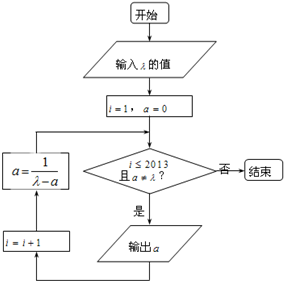 执行下面框图所描述的算法程序,记输出的一列数依次为a1,a2,…,an,n∈N*,n≤2013.
执行下面框图所描述的算法程序,记输出的一列数依次为a1,a2,…,an,n∈N*,n≤2013.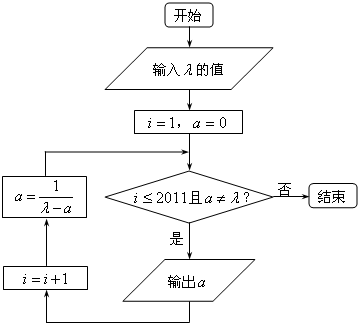 (2011•深圳二模)执行下面框图所描述的算法程序,记输出的一列数依次为a1,a2,…,an,n∈N*,n≤2011.
(2011•深圳二模)执行下面框图所描述的算法程序,记输出的一列数依次为a1,a2,…,an,n∈N*,n≤2011.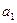 ,
,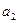 ,…,
,…,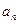 ,
,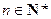 ,
,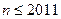 .(注:框图中的赋值符号“
.(注:框图中的赋值符号“ ”也可以写成“
”也可以写成“ ”或“:
”或“: ,写出输出结果;
,写出输出结果; ,令
,令 ,证明
,证明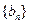 是等差数列,并写出数列
是等差数列,并写出数列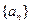 的通项公式;
的通项公式;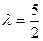 ,令
,令 ,
,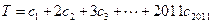 .
.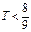 .
.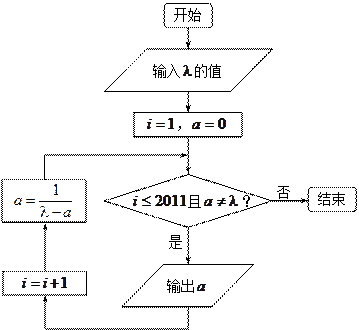
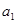 ,
,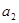 ,…,
,…, ,
, ,
, .
.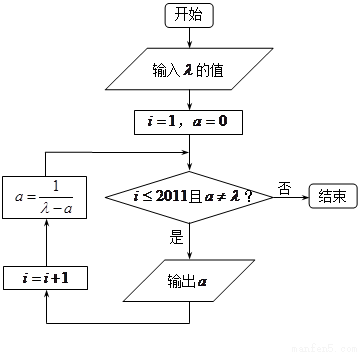
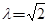 ,写出输出结果;
,写出输出结果; ,求数列
,求数列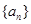 的通项公式;
的通项公式;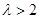 ,令
,令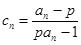 ,求常数
,求常数 (
(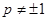 ),使得
),使得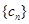 是等比数列.
是等比数列.