题目内容
(5分)(2011•广东)已知集合A={(x,y)|x,y为实数,且x2+y2=1},B=|(x,y)|x,y为实数,且x+y=1},则A∩B的元素个数为( )
| A.4 | B.3 | C.2 | D.1 |
C
试题分析:观察两集合发现,两集合表示两点集,要求两集合交集元素的个数即为求两函数图象交点的个数,所以联立两函数解析式,求出方程组的解,有几个解就有几个交点即为两集合交集的元素个数.
解:联立两集合中的函数关系式得:
 ,
,由②得:x=1﹣y,代入②得:y2﹣y=0即y(y﹣1)=0,解得y=0或y=1,
把y=0代入②解得x=1,把y=1代入②解得x=0,
所以方程组的解为
 或
或 ,有两解,
,有两解,则A∩B的元素个数为2个.
故选C
点评:此题考查学生理解交集的运算,考查了求两函数交点的方法,是一道基础题.本题的关键是认识到两集合表示的是点坐标所构成的集合即点集.

练习册系列答案
相关题目
 ,
, },i是虚数单位,Z为整数集,则集合Z∩M中的元素个数是( )
},i是虚数单位,Z为整数集,则集合Z∩M中的元素个数是( ) ,
, ,则
,则 .
. ,
, ,
, ,则
,则 的值等于 .
的值等于 . ,
, ,则
,则 ( )
( ) 



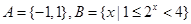 ,则
,则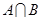 等于( )
等于( ) 等于( )
等于( )


