题目内容
在△ABC中，sinA：sinB：sinC=1：2：
，则∠C=________．
120°
分析：由正弦定理知，可设三边分别为 k，2k，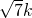
，再由余弦定理可得 7k2=k2+4k2-4k2 cosC，求出cosC的值，结合
C的范围，求出C的大小．
解答：由正弦定理知，可设三边分别为 k，2k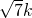，，再由余弦定理可得 7k2=k2+4k2-4k2 cosC，
解得 cosC=-
，又0＜C＜π，∴C=120°，
故答案为：120°．
点评：本题考查正弦定理、余弦定理的应用，根据三角函数的值求角，射出三边分别为 k，2k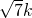，，是解题的关键．
分析：由正弦定理知，可设三边分别为 k，2k，
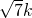，再由余弦定理可得 7k2=k2+4k2-4k2 cosC，求出cosC的值，结合C的范围，求出C的大小．
解答：由正弦定理知，可设三边分别为 k，2k，
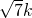，再由余弦定理可得 7k2=k2+4k2-4k2 cosC，解得 cosC=-
，又0＜C＜π，∴C=120°，故答案为：120°．
点评：本题考查正弦定理、余弦定理的应用，根据三角函数的值求角，射出三边分别为 k，2k，
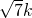，是解题的关键． 
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
在△ABC中，“sin（A-B）cosB+cos（A-B）sinB≥1”是“△ABC是直角三角形”的（ ）
| A、充分不必要条件 | B、必要不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |