题目内容
已知函数 ,其中
,其中 为常数.
为常数.
(1)求函数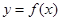 的周期;
的周期;
(2)如果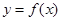 的最小值为
的最小值为 ,求
,求 的值,并求此时
的值,并求此时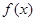 的最大值及图像的对称轴方程.
的最大值及图像的对称轴方程.
(1) ,(2)
,(2) ,最大值等于4,
,最大值等于4,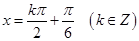
解析试题分析:(1)研究三角函数性质,首先将其化为基本三角函数,即化为形如: ,由倍角公式,降幂公式及配角公式得:
,由倍角公式,降幂公式及配角公式得: ,然后利用基本三角函数性质进行求解,即
,然后利用基本三角函数性质进行求解,即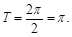 (2)由
(2)由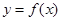 的最小值为
的最小值为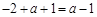 ,得
,得 ,因此最大值为
,因此最大值为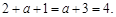 对称轴方程满足:
对称轴方程满足: 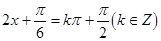 ,即:
,即: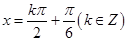 .
.
试题解析:解(1)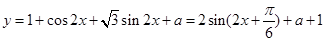 . 4分
. 4分 . 6分
. 6分
(2)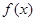 的最小值为
的最小值为 ,所以
,所以 故
故 8分
8分
所以函数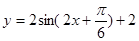 .最大值等于4 10分
.最大值等于4 10分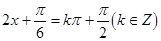 ,即
,即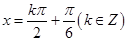 时函数有最大值或最小值,
时函数有最大值或最小值,
故函数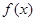 的图象的对称轴方程为
的图象的对称轴方程为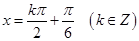 . 14分
. 14分
考点:三角函数性质,三角函数式化简

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目

 的最小正周期;
的最小正周期;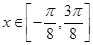 时,求函数f(x)的单调区间。
时,求函数f(x)的单调区间。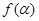 =
=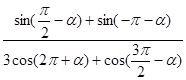 ; (2)若
; (2)若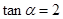 ,求
,求
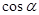 的值;
的值;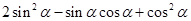 的值.
的值. ,设函数
,设函数 .
. ,且
,且 恰是函数f(x)在
恰是函数f(x)在 上的最大值,求A,b和三角形ABC的面积.
上的最大值,求A,b和三角形ABC的面积. .
. 的定义域及最小正周期;
的定义域及最小正周期;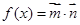 ,其中向量
,其中向量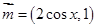 ,
,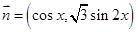 ,
, .
. 的单调递增区间;
的单调递增区间;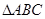 中,
中,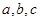 分别是角
分别是角 的对边,已知
的对边,已知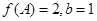 ,
,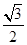 ,求
,求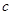 的值.
的值.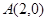 ,
,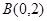 ,
,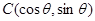 ,
,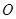 为坐标原点.
为坐标原点.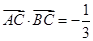 ,求
,求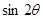 的值;
的值;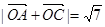 ,且
,且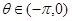 ,求
,求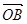 与
与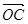 的夹角.
的夹角.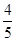 ,求S△AOB.
,求S△AOB.