题目内容
1．已知抛物线y2=6x，过焦点F的直线与抛物线交于A，B两点，过A，B分别作y轴的垂线，垂足分别为C，D，则|AC|+|BD|的最小值为3．分析 求得抛物线的焦点和准线方程，由抛物线的定义，可得|AC|+|BD|=|AF|+|BF|-1=|AB|-1，求得|AB|的最小值即可．
解答 解：抛物线y2=6x的焦点F（$\frac{3}{2}$，0），准线方程为x=-$\frac{3}{2}$，
由抛物线的定义可得，|AF|=|AC|+$\frac{3}{2}$，|BF|=|BD|+$\frac{3}{2}$，
即有|AC|+|BD|=|AF|+|BF|-3=|AB|-3，
当直线AB⊥x轴时，|AB|最小．
令x=$\frac{3}{2}$，则y2=9，解得y=±3，
即有|AB|min=6，
则|AC|+|BD|的最小值为3．
故答案为：3．
点评 本题考查抛物线的定义、方程和性质，主要考查定义法及运算能力，属于中档题．
练习册系列答案
相关题目
11．若存在非零实数x，y，使不等式（6a-1）x2-2xy+ay2≥0成立，则实数a的取值范围是（ ）
| A． | [0，+∞） | B． | （-∞-$\frac{1}{3}$）∪（$\frac{1}{2}$，+∞） | C． | [-$\frac{1}{3}$，+∞） | D． | [$\frac{1}{2}$，+∞） |
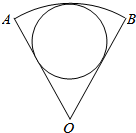如图所示：“十字形”公路的交叉处周围呈扇形形状，某市规划拟在这块扇形土尘修建一个圆形广扬，已知∠A0B=60°，AB的长度=100πm，怎样设计广场的占地面积最大？其值是多少？
16．
如图是底面积为$\sqrt{3}$，体积为$\sqrt{3}$的正三棱锥的主视图（等腰三角形）和左视图（等边三角形），此正三棱锥的侧视图的面积为（ ）
如图是底面积为$\sqrt{3}$，体积为$\sqrt{3}$的正三棱锥的主视图（等腰三角形）和左视图（等边三角形），此正三棱锥的侧视图的面积为（ ）| A． | $\frac{3\sqrt{3}}{2}$ | B． | 3 | C． | $\sqrt{3}$ | D． | $\frac{3}{2}$ |