Question

（05年全国卷Ⅰ）（14分）

已知椭圆的中心为坐标原点O，焦点在轴上，斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点，与共线。

（Ⅰ）求椭圆的离心率；

（Ⅱ）设M为椭圆上任意一点，且，证明为定值。

Answer 1

解析：（1）解：设椭圆方程为

则直线AB的方程为，代入，化简得

.

令A（），B），则

由与共线，得

又，

即，所以，

故离心率

（II）证明：（1）知，所以椭圆可化为

设，由已知得

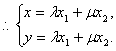
 在椭圆上，

即①

由（1）知

又，代入①得

故为定值，定值为1.