题目内容
已知y=sin(ωx+?)与直线y=
的交点中,距离最近的两点间的距离为
,那么此函数的最小正周期是( )
| 1 |
| 2 |
| π |
| 3 |
分析:利用sin(ωx+φ)=
,可得到ωx1+φ=2kπ+
,ωx2+φ=2kπ+
,两式相减,结合题意可求得ω,从而可得选项.
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
解答:解:∵sin(ωx+φ)=
,
∴ωx1+φ=2kπ+
,(1)
ωx2+φ=2kπ+
,(2)
(2)-(1)得:ω(x2-x1)=
;
∵|x2-x1|=
,
∴ω•
=
,
∴ω=2;
∴周期T=
=π.
故选C.
| 1 |
| 2 |
∴ωx1+φ=2kπ+
| π |
| 6 |
ωx2+φ=2kπ+
| 5π |
| 6 |
(2)-(1)得:ω(x2-x1)=
| 2π |
| 3 |
∵|x2-x1|=
| π |
| 3 |
∴ω•
| π |
| 3 |
| 2π |
| 3 |
∴ω=2;
∴周期T=
| 2π |
| 2 |
故选C.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,关键是根据sin(ωx+?)=
求得ωx1+φ与ωx2+φ的式子,再结合题意求得ω,属于中档题.
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的交点中,距离最近的两点间的距离为
的交点中,距离最近的两点间的距离为 ,那么此函数的最小正周期是
,那么此函数的最小正周期是
 的交点中,距离最近的两点间的距离为
的交点中,距离最近的两点间的距离为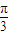 ,那么此函数的最小正周期是( )
,那么此函数的最小正周期是( )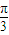
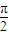
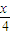 ,则方程f(x)=
,则方程f(x)= 的解集为 .
的解集为 .