题目内容
已知y=f(x)是周期为2π的函数,当x∈(0,2π)时,f(x)=sin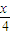 ,则方程f(x)=
,则方程f(x)= 的解集为 .
的解集为 .
【答案】分析:先根据函数在区间(0,2π)上的解析式,求出方程的一个根,再根据函数的周期性求出方程在定义域上的所有根的集合.
解答:解:由题意知,当x∈(0,2π)时,f(x)=sin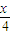 ,
,
∴当x∈(0,2π)时,由sin =
= ,得
,得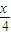 =
=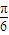 ,即x=
,即x= π,
π,
又∵f(x)的周期为2π,
∴f(x)= 的解集为{x|x=2kπ+
的解集为{x|x=2kπ+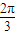 ,k∈Z},
,k∈Z},
故答案为:{x|x=2kπ+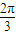 ,k∈Z}.
,k∈Z}.
点评:本题考查了三角函数方程的解法以及周期性的应用,即根据正弦(余弦)函数的图象求出在一个周期上的根,在根据周期求出方程的解集.
解答:解:由题意知,当x∈(0,2π)时,f(x)=sin
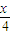 ,
,∴当x∈(0,2π)时,由sin
 =
= ,得
,得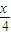 =
=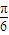 ,即x=
,即x= π,
π,又∵f(x)的周期为2π,
∴f(x)=
 的解集为{x|x=2kπ+
的解集为{x|x=2kπ+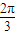 ,k∈Z},
,k∈Z},故答案为:{x|x=2kπ+
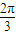 ,k∈Z}.
,k∈Z}.点评:本题考查了三角函数方程的解法以及周期性的应用,即根据正弦(余弦)函数的图象求出在一个周期上的根,在根据周期求出方程的解集.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
(2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论: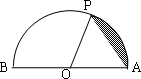
 已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论: