题目内容
已知圆C:(x-a.)2+(y-b)2=r2,求与圆C相切于点P0(x0,y0)的切线方程(如图2).
图2
解:设P(x,y)为所求直线l上一点.
根据圆的切线性质,有![]() ⊥l,即
⊥l,即![]() ·
·![]() =0.
=0.
因为![]() =(x0-a.,y0-b),
=(x0-a.,y0-b),![]() =(x-x0,y-y0),
=(x-x0,y-y0),
所以(x0-a)(x-x0)+(y0-b)(y-y0)=0.
特别地,当圆心在坐标原点时,圆的标准方程为x2+y2=r2,与它相切于P0(x0,y0)的切线方程为x0(x-x0)+y0(y-y0)=0,
由于x02+y02=r2,故此方程可化为x0x+y0y=r2.
由解析几何,知给定斜率为k的直线l,则向量m=(1,k)与直线l共线,我们把与直线l共线的非零向量m称为直线l的方向向量.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
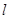 :x-y+3=0,当直线
:x-y+3=0,当直线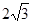 时,则a=
时,则a=